堆

了解堆结构和堆排序

知识点

数组去重的几种方式

1.利用 ES6 Set 去重（ES6 中最常用）

1
2
3
function unique (arr) {
  return Array.from(new Set(arr))
}

2、利用 for 嵌套 for，然后 splice 去重（ES5 中最常用）

1
2
3
4
5
6
7
8
9
10
11
function unique(arr){            
        for(var i=0; i<arr.length; i++){
            for(var j=i+1; j<arr.length; j++){
                if(arr[i]==arr[j]){         //第一个等同于第二个
                    arr.splice(j,1);		//splice方法删除第二个
                    j--;
                }
            }
        }
return arr;
}

3.利用 indexOf 去重

1
2
3
4
5
6
7
8
9
10
function unique(arr) {
    var array = [];
    for (var i = 0; i < arr.length; i++) {
        if (array.indexOf(arr[i]) === -1) {
            array.push(arr[i])
        }
    }
    return array;
}

4.利用 includes

1
2
3
4
5
6
7
8
9
10
11
12
13
function unique(arr) {
    if (!Array.isArray(arr)) {
        console.log('type error!')
        return
    }
    var array =[];
    for(var i = 0; i < arr.length; i++) {
            if( !array.includes(arr[i]) ) {//includes 检测数组是否有某个值
                    array.push(arr[i]);
              }
    }
    return array
}

5.利用 Map 数据结构去重

1
2
3
4
5
6
7
8
9
10
11
12
13
function arrayNonRepeatfy(arr) {
  let map = new Map();
  let array = new Array();  // 数组用于返回结果
  for (let i = 0; i < arr.length; i++) {
    if(map.has(arr[i])) {  // 如果有该key值
      map.set(arr[i], true); 
    } else { 
      map.set(arr[i], false);   // 如果没有该key值
      array.push(arr[i]);
    }
  } 
  return array ;
}

6.[…new Set(arr)]

1
2
[...new Set(arr)] 
//代码就是这么少----（其实，严格来说并不算是一种，相对于第一种方法来说只是简化了代码）

二分法两种方式

二分法第一种写法

第一种写法，我们定义 target 是在一个在左闭右闭的区间里，也就是[left, right] （这个很重要非常重要）。

区间的定义这就决定了二分法的代码应该如何写，因为定义target在[left, right]区间，所以有如下两点：

  • while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
  • if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1

例如在数组：1,2,3,4,7,9,10中查找元素2，如图所示：

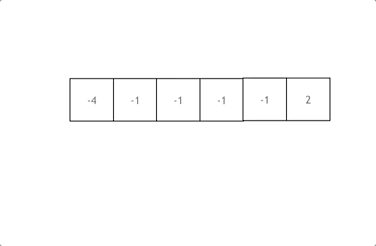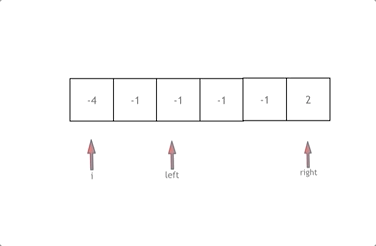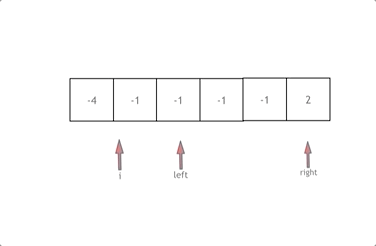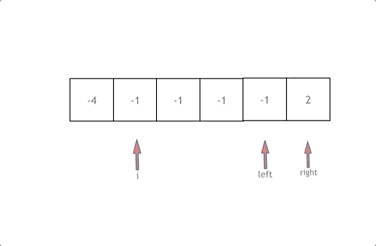
二分法第二种写法

如果说定义 target 是在一个在左闭右开的区间里，也就是[left, right) ，那么二分法的边界处理方式则截然不同。

有如下两点：

  • while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
  • if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]

在数组：1,2,3,4,7,9,10中查找元素2，如图所示：（注意和方法一的区别）

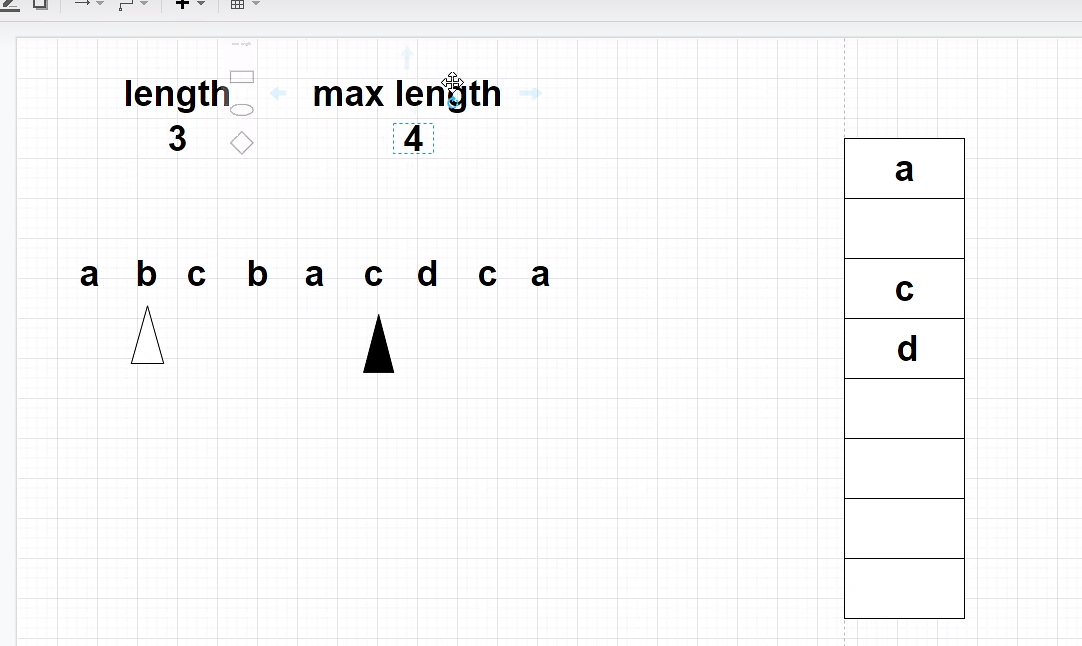
CodeTop 前端高频 60

0.模板

题目

解法：

无重复字符的最长子串

题目：

解法：

1.滑动窗口法

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
var lengthOfLongestSubstring = function(s) {
  let left = right = length = maxlength = 0;
  let set = new Set();
  while (right < s.length) {
      if (!set.has(s[right])) {
          set.add(s[right]);
          length++;
          right++;
          if(length>maxlength){
            maxlength = length;
          }
      }else {
        while(set.has(s[right])){
            set.delete(s[left]);
            left++;
            length--;
        }
         set.add(s[right]);
         length++;
         right++;
      }
    }
  return maxlength;
};

多思考。。。

合并两个有序数组

题目

解法：

1.合并数组再比较
1
2
3
4
5
var merge = function(nums1, m, nums2, n) {
  // 123256
  nums1.splice(m,nums1.length-m,...nums2)
  nums1.sort((a,b)=>a-b)
};

这里需要用到 splice

splice

splice(start, deleteCount, item1, item2……)

  • start参数 开始的位置
  • deleteCount要截取的个数
  • 后面的**items为要添加的元素**
  • 如果deleteCount为0，则表示不删除元素，从start位置开始添加后面的几个元素到原始的数组里面。
  • 返回值为由被删除的元素组成的一个数组。如果只删除了一个元素，则返回只包含一个元素的数组。如果没有删除元素，则返回空数组。
  • 这个方法会改变原始数组，数组的长度会发生变化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
const arr3 = [1, 2, 3, 4, 5, 6, 7, "f1", "f2"];
const arr4 = arr3.splice(2, 3) // 删除第三个元素以后的三个数组元素(包含第三个元素)
console.log(arr4); // [3, 4, 5];
console.log(arr3); // [1, 2, 6, 7, "f1", "f2"]; 原始数组被改变

const arr5 = arr3.splice(2, 0, "wu", "leon"); 
// 从第2位开始删除0个元素，插入"wu","leon"
console.log(arr5); // [] 返回空数组
console.log(arr3); // [1, 2, "wu", "leon", 6, 7, "f1", "f2"]; 原始数组被改变

const arr6 = arr3.splice(2, 3, "xiao", "long");
// 从第 2 位开始删除 3 个元素，插入"xiao", "long"
console.log(arr6); // ["wu", "leon", 6]
console.log(arr3); //[ 1, 2, "xiao", "long", 7, "f1", "f2"]

const arr7 = arr3.splice(2); // 从第三个元素开始删除所有的元素
console.log(arr7);// ["xiao", "long", 7, "f1", "f2"]
console.log(arr3); // [1, 2]


sort()

  • 对数组的元素进行排序，并返回数组。
  • 默认排序顺序是在将元素转换为字符串，然后比较它们的UTF-16代码单元值序列时构建的。
1
2
3
const arr = [1, 2, 3]
arr.sort((a, b) => b - a)
console.log(arr) // [3, 2, 1]
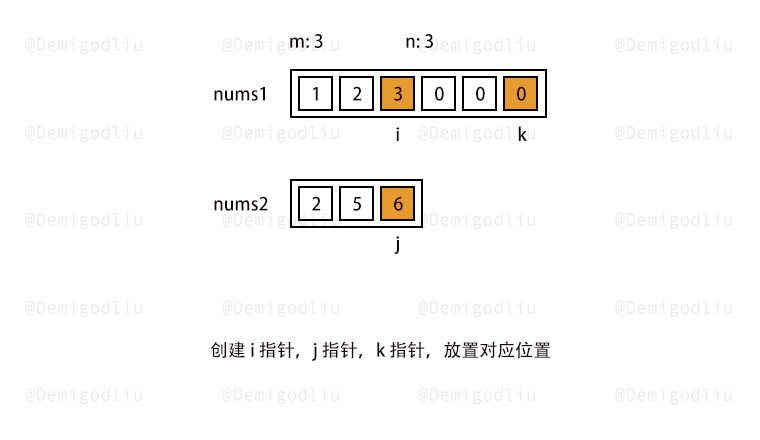
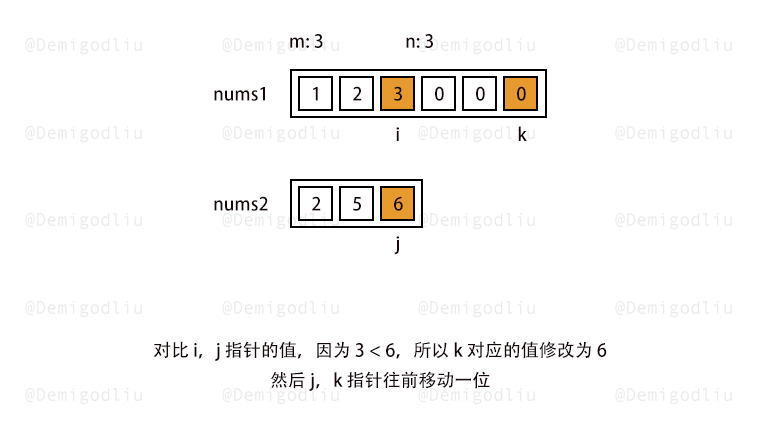
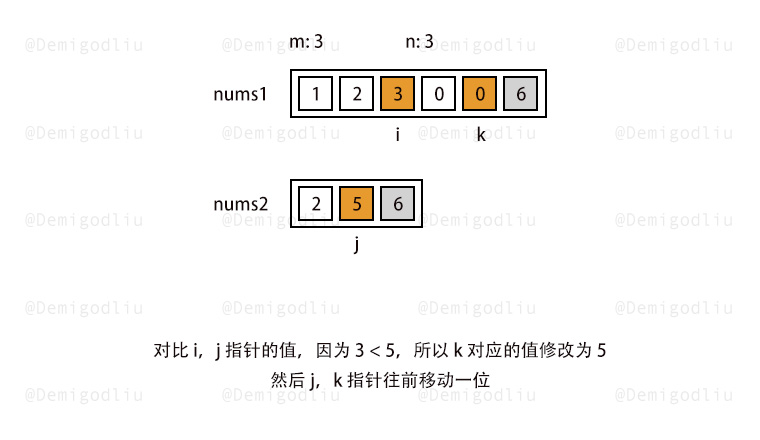
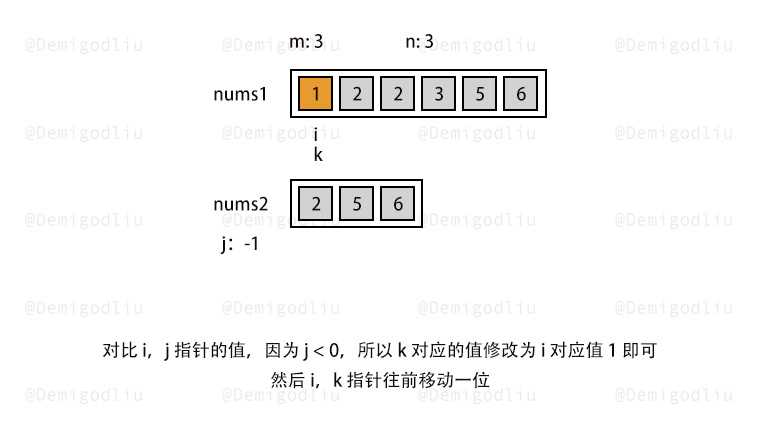
2.双指针从后遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
let a1 = [1,2,4,0,0,0,0,0,0]
let a2 = [3,5]


var merge = function(nums1, m, nums2, n) {
    // 123256
    let t = m - 1,k = n - 1;
    let j = m + n - 1
    while(t>=0 || k >=0){
        if(t<0){
            nums1[j] = nums2[k];
            j--;
            k--;
        }
         else if(k<0){
            nums1[j] = nums1[t];
            j--;
            t--;
        }
         else if(nums1[t]>nums2[k]){
            nums1[j] = nums1[t];
            j--;
            t--;
        }else {
            nums1[j] = nums2[k];
            j--;
            k--;
        }
    }
    return nums1;
};

console.log(merge(a1,3,a2,2));

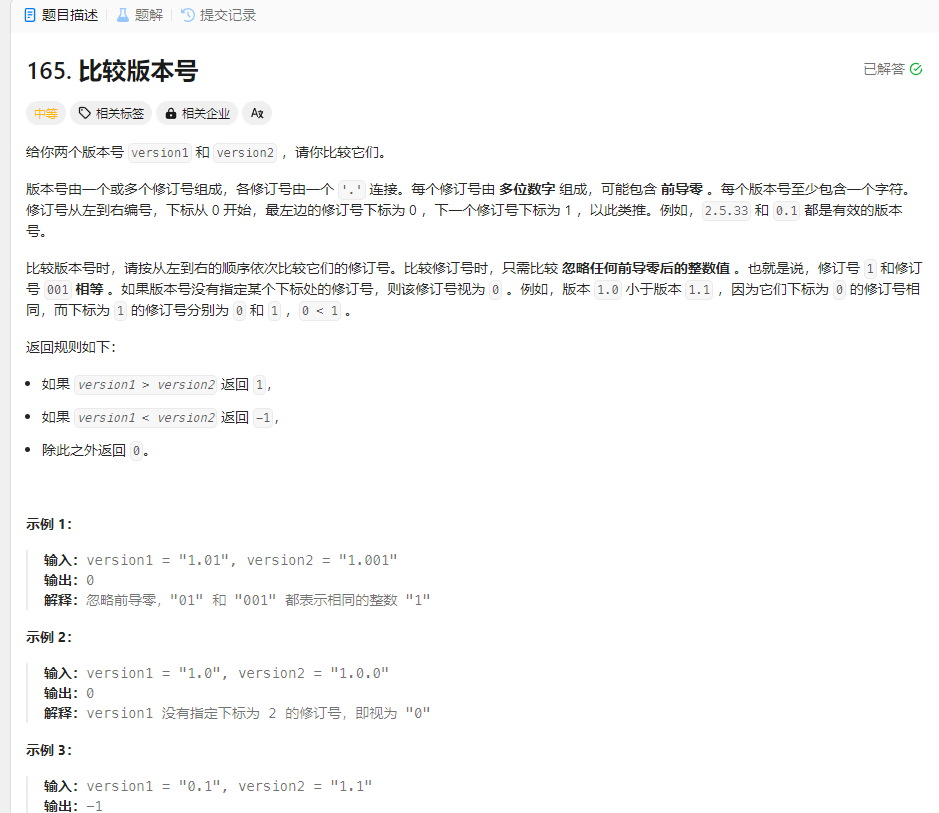
比较版本号

题目

解法：

1.分割字符法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
var compareVersion = function(version1, version2) {

    let l1 = version1.split('.');
    let l2 = version2.split('.');
    let l1num = l1.map(item=>parseInt(item))
    let l2num = l2.map(item=>parseInt(item))
    console.log(l1num,l2num);
    for(let i = 0 ;i< (l1.length>l2.length?l1.length:l2.length);i++ ){
        let x = l1num[i];
        let y = l2num[i];
        if(x == undefined){
            x = 0
        }
        if(y == undefined){
            y = 0
        }
        if(x>y){
            return 1;
        }else if(x<y){
            return -1;
        }
    }
    return 0;
};

spilt

使用指定的分隔符将一个字符串拆分为多个子字符串数组并返回，原字符串不变。

1
2
const str = 'A*B*C*D*E*F*G'
console.log(str.split('*')) // 输出 ["A", "B", "C", "D", "E", "F", "G"]

shift()

在头部弹出数据，原数组会变。数组的 push（入队） & shift（出队） 可以模拟常见数据结构之一：队列。

1
2
3
4
5
6
7
8
9
10
11
12
13
const arr = [1, 2, 3]
const shiftVal = arr.shift()
console.log(shiftVal) // 1
console.log(arr) // [2, 3]

// 数组模拟常见数据结构之一：队列
const queue = [0, 1]
queue.push(2) // 入队
console.log(queue) // [0, 1, 2]

const shiftValue = queue.shift() // 出队
console.log(shiftValue) // 0
console.log(queue) // [1, 2]

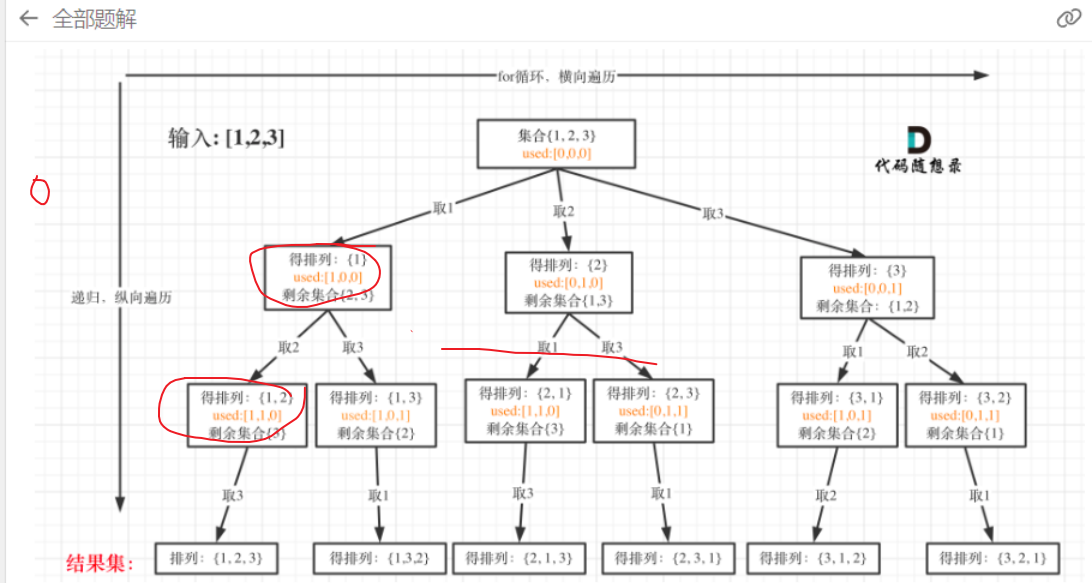
全排列

题目

解法：

1.回溯算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
var permute = function(nums) {
    const res = [], path = [];
    backtracking(nums, nums.length, []);
    return res;
    
    function backtracking(n, k, used) {
        if(path.length === k) {
            res.push(Array.from(path));
            return;
        }
        for (let i = 0; i < k; i++ ) {
            if(used[i]) continue;
            path.push(n[i]);
            used[i] = true; // 同支
            backtracking(n, k, used);
            path.pop();
            used[i] = false;
        }
    }
};

最大子数组和

题目

解法：

1.动态规划

动态规划压缩时间，将dp[]数组用一个滚动量pre来表示，节约空间

具体思路可看：算法讲解070【必备】子数组最大累加和问题与扩展-上_哔哩哔哩_bilibili

1
2
3
4
5
6
7
8
9
10
11
12
var maxSubArray = function(nums) {
    let pre = nums[0]
    let max = nums[0];
    for(let i = 1;i<nums.length;i++){
        pre = Math.max(pre+nums[i],nums[i]);
        max = Math.max(pre,max)

       
    }
    return max

};

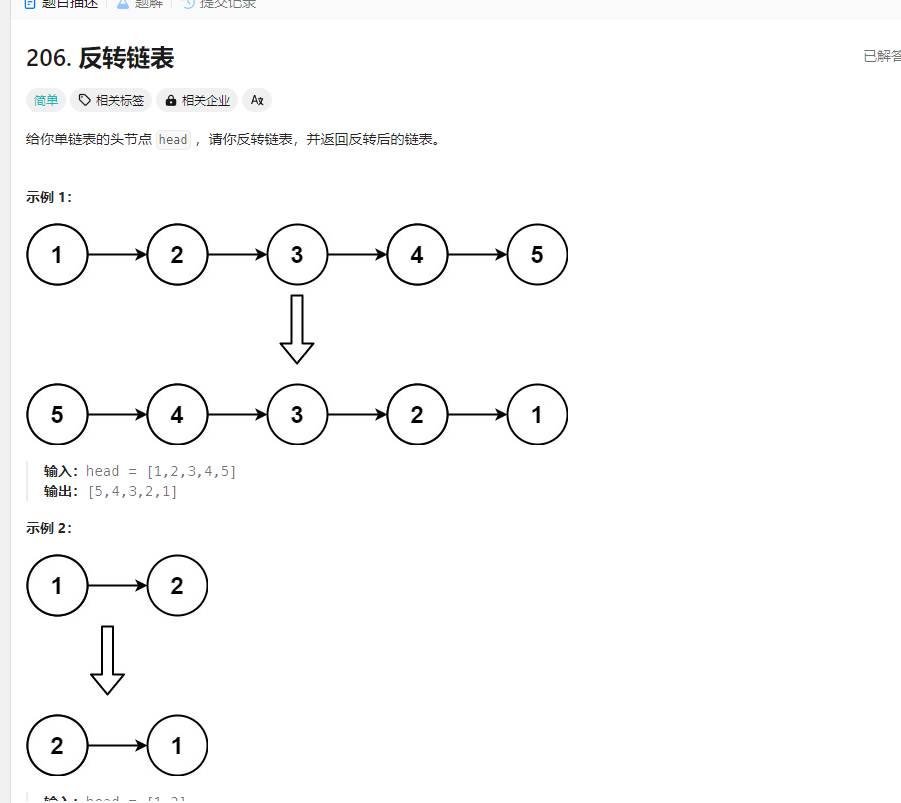
反转链表

题目

解法：

1.双指针加一个临时变量

注意：只要思考改变指向关系和节点的移动就可以了，改变两个节点的指向时为了防止丢失用临时变量存储下一个节点

1
2
3
4
5
6
7
8
9
10
var reverseList = function(head) {
    let pre = null;
    let cur = head;
    while(cur != null){
        let temp = cur.next
        cur.next = pre;
        pre = cur;
        cur = temp;
    }
};

三数之和

题目

解法：

1.双指针法

梦破碎的地方！| LeetCode：15.三数之和_哔哩哔哩_bilibili

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
var threeSum = function(nums) {
    const res = [], len = nums.length
    // 将数组排序
    nums.sort((a, b) => a - b)
    for (let i = 0; i < len; i++) {
        let l = i + 1, r = len - 1, iNum = nums[i]
        // 数组排过序，如果第一个数大于0直接返回res
        if (iNum > 0) return res
        // 去重
        if (iNum == nums[i - 1]) continue
        while(l < r) {
            let lNum = nums[l], rNum = nums[r], threeSum = iNum + lNum + rNum
            // 三数之和小于0，则左指针向右移动
            if (threeSum < 0) l++ 
            else if (threeSum > 0) r--
            else {
                res.push([iNum, lNum, rNum])
                // 去重
                while(l < r && nums[l] == nums[l + 1]){
                    l++
                }
                while(l < r && nums[r] == nums[r - 1]) {
                    r--
                }
                l++
                r--
            }
        }
    }
    return res
};

关键在于去重

很多同学写本题的时候，去重的逻辑多加了 对right 和left 的去重：（代码中注释部分）

1
2
3
4
5
6
7
8
9
10
11
12
while (right > left) {
    if (nums[i] + nums[left] + nums[right] > 0) {
        right--;
        // 去重 right
        while (left < right && nums[right] == nums[right + 1]) right--;
    } else if (nums[i] + nums[left] + nums[right] < 0) {
        left++;
        // 去重 left
        while (left < right && nums[left] == nums[left - 1]) left++;
    } else {
    }
}

但细想一下，这种去重其实对提升程序运行效率是没有帮助的。

拿right去重为例，即使不加这个去重逻辑，依然根据 while (right > left) 和 if (nums[i] + nums[left] + nums[right] > 0) 去完成right– 的操作。

多加了 while (left < right && nums[right] == nums[right + 1]) right--; 这一行代码，其实就是把 需要执行的逻辑提前执行了，但并没有减少 判断的逻辑。

最直白的思考过程，就是right还是一个数一个数的减下去的，所以在哪里减的都是一样的。

所以这种去重 是可以不加的。 仅仅是 把去重的逻辑提前了而已。

#思考题

既然三数之和可以使用双指针法，我们之前讲过的1.两数之和 (opens new window)，可不可以使用双指针法呢？

两数之和 就不能使用双指针法，因为1.两数之和 (opens new window)要求返回的是索引下标， 而双指针法一定要排序，一旦排序之后原数组的索引就被改变了。

如果1.两数之和 (opens new window)要求返回的是数值的话，就可以使用双指针法了。

移除元素

题目

解法：

1.双指针法

定义快慢指针

  • 快指针：寻找新数组的元素 ，新数组就是不含有目标元素的数组
  • 慢指针：指向更新 新数组下标的位置

1
2
3
4
5
6
7
8
9
10
var removeElement = function(nums, val) {
    let slowindex = 0;
    for(let fastindex = 0;fastindex<nums.length;fastindex++){
        if(val!=nums[fastindex]){
            nums[slowindex] == nums[fastindex];
            slowindex++
        }
    }
    return slowindex
};

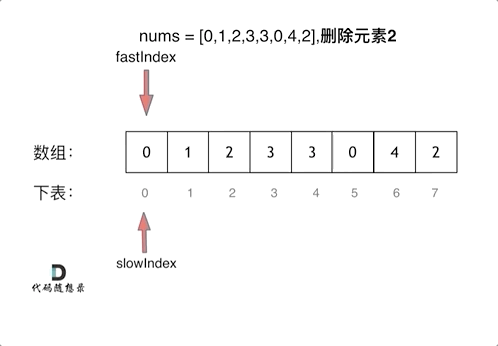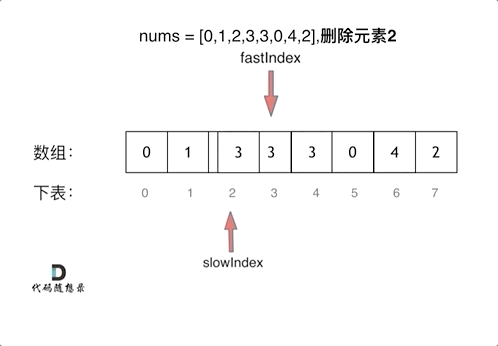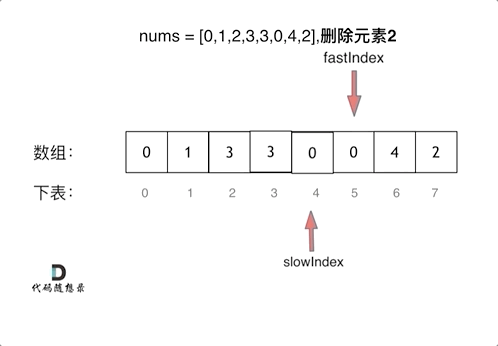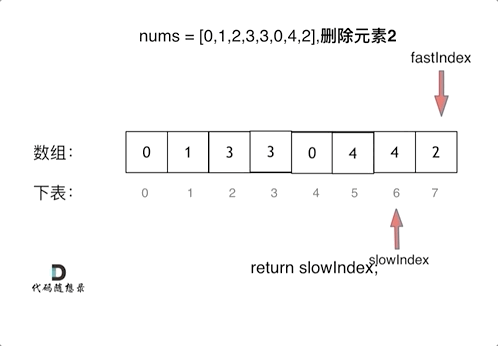
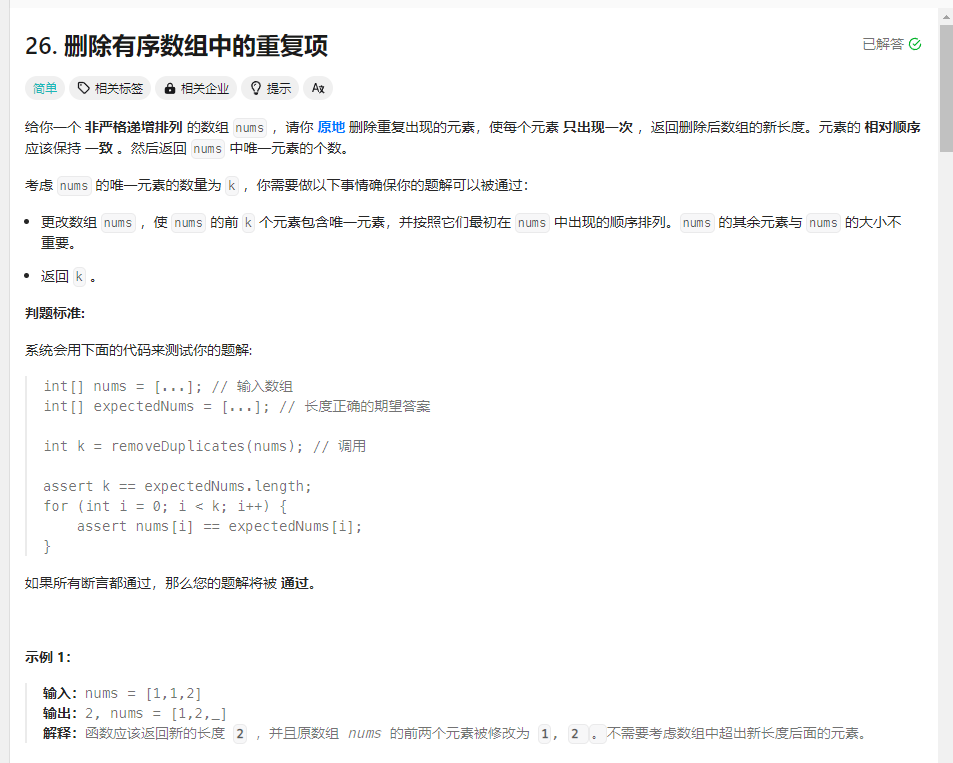
删除有序数组中的重复项

题目

解法：

1.双指针法
1
2
3
4
5
6
7
8
9
10
var removeDuplicates = function(nums) {
    let  slow = 0;
    for(fast = 1;fast<nums.length;fast++){
        if(nums[fast] != nums[slow]){
            nums[slow] = nums[fast];
            slow++
        }
    }
    return slow;
};

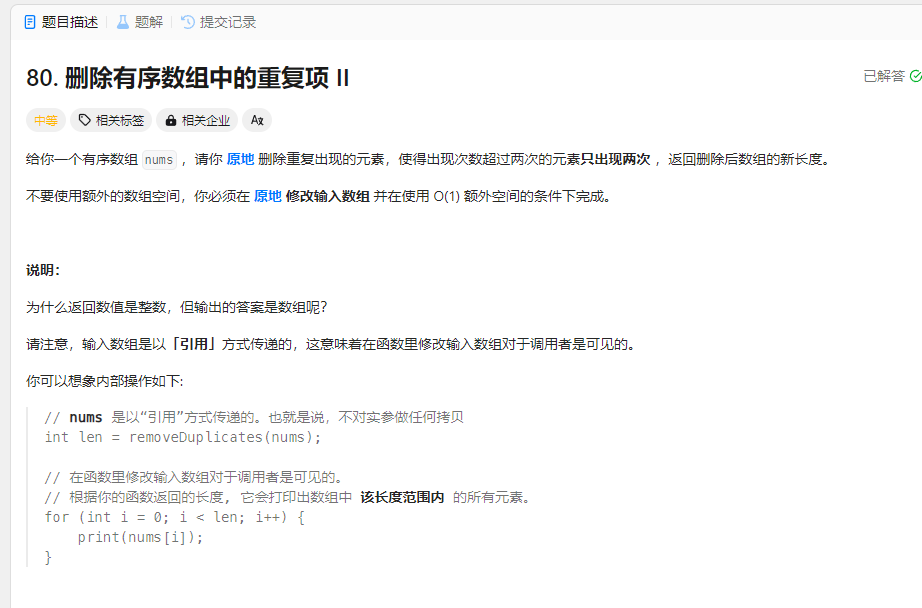
删除排序数组中的重复项 II

题目

解法：

1.双指针法

参考80. 删除有序数组中的重复项 II_哔哩哔哩_bilibili

1
2
3
4
5
6
7
8
9
10
11
12
13
14
var removeDuplicates = function(nums) {
     const n = nums.length;
    if (n <= 2) {
        return n;
    }
    let slow = 2;
    for(let fast = 2;fast<nums.length;fast++){
        if(nums[fast] != nums[slow-2]){
          nums[slow] = nums[fast];
            ++slow;
        }
    }
     return slow;
};

长度最小的子数组

题目

解法：

1.双指针法

接下来就开始介绍数组操作中另一个重要的方法：滑动窗口。

所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。

在暴力解法中，是一个for循环滑动窗口的起始位置，一个for循环为滑动窗口的终止位置，用两个for循环 完成了一个不断搜索区间的过程。

那么滑动窗口如何用一个for循环来完成这个操作呢。

首先要思考 如果用一个for循环，那么应该表示 滑动窗口的起始位置，还是终止位置。

如果只用一个for循环来表示 滑动窗口的起始位置，那么如何遍历剩下的终止位置？

此时难免再次陷入 暴力解法的怪圈。

所以 只用一个for循环，那么这个循环的索引，一定是表示 滑动窗口的终止位置。

那么问题来了， 滑动窗口的起始位置如何移动呢？

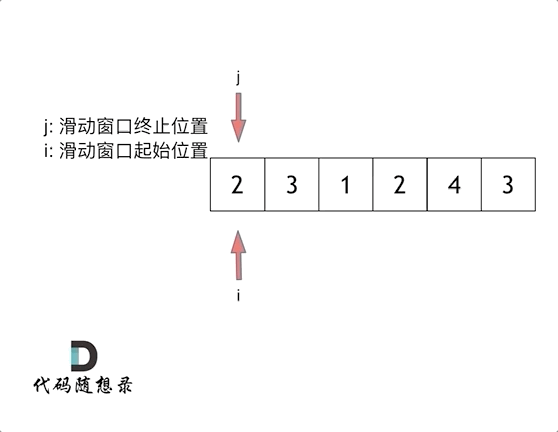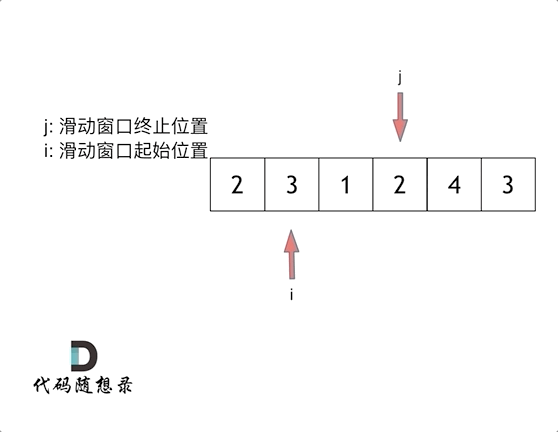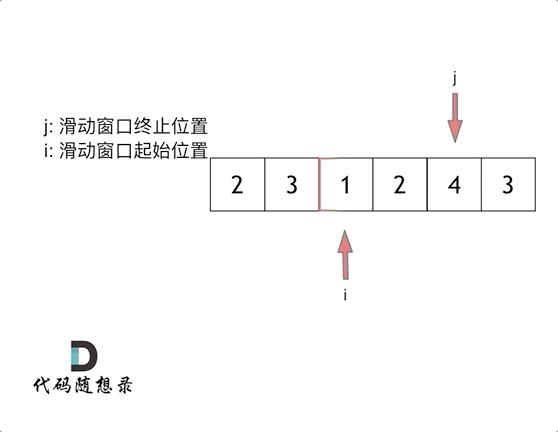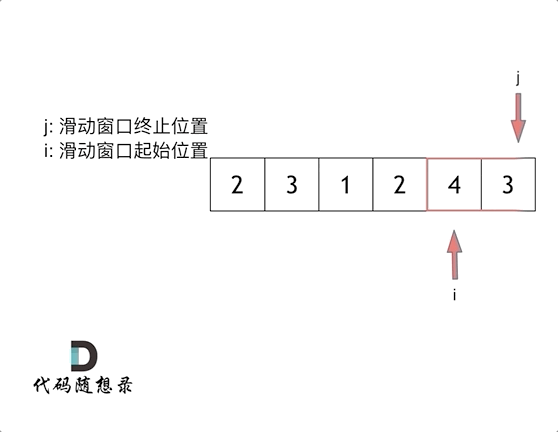
这里还是以题目中的示例来举例，s=7， 数组是 2，3，1，2，4，3，来看一下查找的过程：在本题中实现滑动窗口，主要确定如下三点：

  • 窗口内是什么？
  • 如何移动窗口的起始位置？
  • 如何移动窗口的结束位置？

窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。

窗口的起始位置如何移动：如果当前窗口的值大于s了，窗口就要向前移动了（也就是该缩小了）。

窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
var minSubArrayLen = function(target, nums) {
    let k = nums.length;
    let minlength = Infinity;
    let sum = 0;
    for(let i = 0,j=0;i<k;i++){
        sum += nums[i];
        while(sum>=target){
            if(minlength>i-j+1){
                minlength = i-j+1;
            }  
            sum -= nums[j];
            j++;
        }
    }
    return minlength === Infinity?0:minlength;
};

移除链表元素

题目

解法：

1.虚拟头结点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

var removeElements = function(head, val) {
    //初始化一个虚拟头节点
    const ret = new ListNode(0, head);
    //用临时指针来遍历，不能用head
    let cur = ret;
    while(cur.next) {
        if(cur.next.val === val) {
            cur.next =  cur.next.next;
            continue;
        }
        cur = cur.next;
    }
    //这里要返回虚拟头节点的next，因为head可能被删除了
    return ret.next;
};

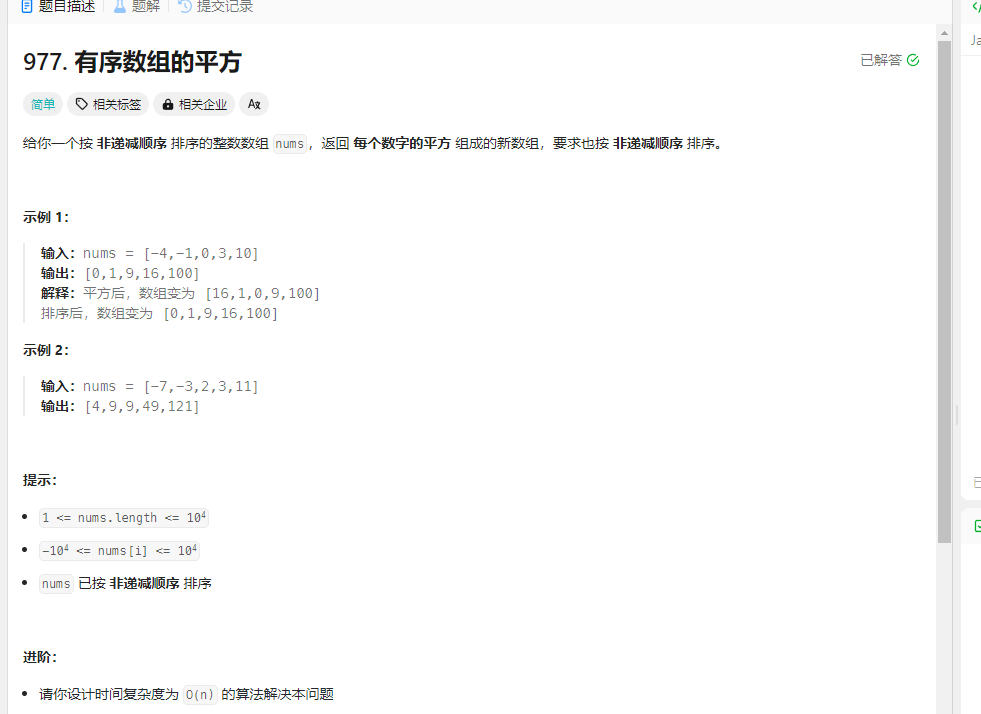
有序数组的平方

题目

解法：

1.双指针法

数组其实是有序的， 只不过负数平方之后可能成为最大数了。

那么数组平方的最大值就在数组的两端，不是最左边就是最右边，不可能是中间。

此时可以考虑双指针法了，i指向起始位置，j指向终止位置。

定义一个新数组result，和A数组一样的大小，让k指向result数组终止位置。

如果A[i] * A[i] < A[j] * A[j] 那么result[k--] = A[j] * A[j]; 。

如果A[i] * A[i] >= A[j] * A[j] 那么result[k--] = A[i] * A[i]; 。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
var sortedSquares = function(nums) {
    let k = nums.length-1;
    let res = new Array(nums.length).fill(0);
    let i = 0,j = nums.length-1;
    while(i<=j){
        if(nums[i]*nums[i]<nums[j]*nums[j]){
            res[k] = nums[j]*nums[j];
            k--; 
            j--;
        }else{
            res[k] = nums[i]*nums[i];
            k--;
            i++;
        }
    }
    return res
};

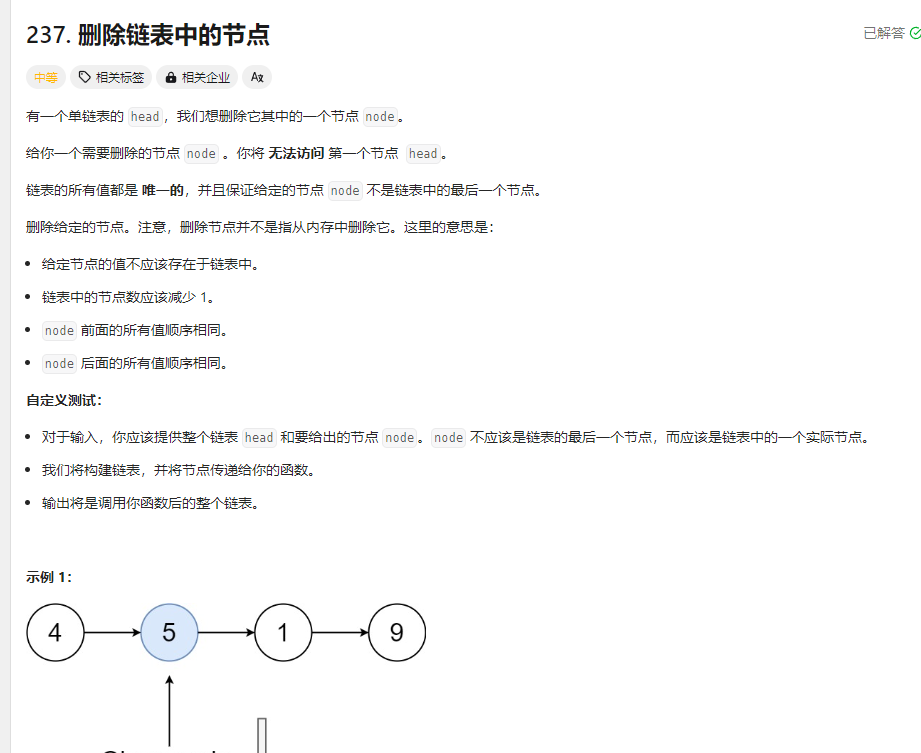
删除链表中的节点

题目

解法：

1.替换
1
2
3
4
var deleteNode = function(node) {
    node.val = node.next.val;
    node.next = node.next.next;
};

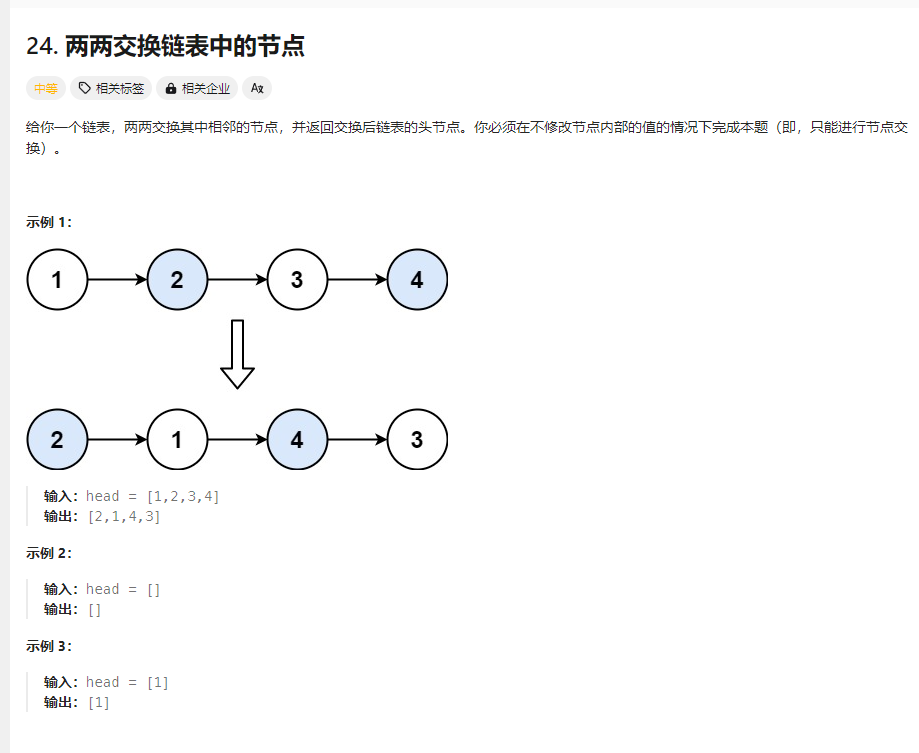
两两交换链表中的节点

题目

解法：

这道题目正常模拟就可以了。

建议使用虚拟头结点，这样会方便很多，要不然每次针对头结点（没有前一个指针指向头结点），还要单独处理。

对虚拟头结点的操作，还不熟悉的话，可以看这篇链表：听说用虚拟头节点会方便很多？ (opens new window)。

接下来就是交换相邻两个元素了，此时一定要画图，不画图，操作多个指针很容易乱，而且要操作的先后顺序

初始时，cur指向虚拟头结点，然后进行如下三步：

操作之后，链表如下：

看这个可能就更直观一些了：

1.虚拟头节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
var swapPairs = function(head) {
    const ret = new ListNode(0, head);
    let cur = ret;
    
    while (cur.next && cur.next.next) {
        let temp = cur.next;
        let temp2 = cur.next.next;
        
        // 交换节点
        cur.next = temp2;
        temp.next = temp2.next;
        temp2.next = temp;
        
        // 移动到下一对节点
        cur = temp;
    }
    
    return ret.next;
};

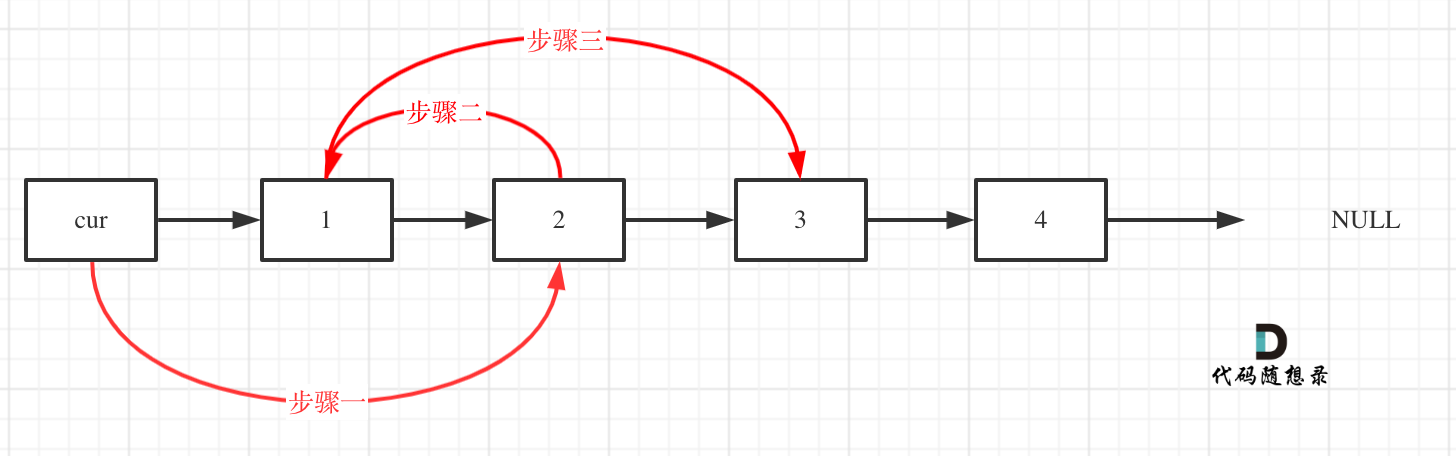
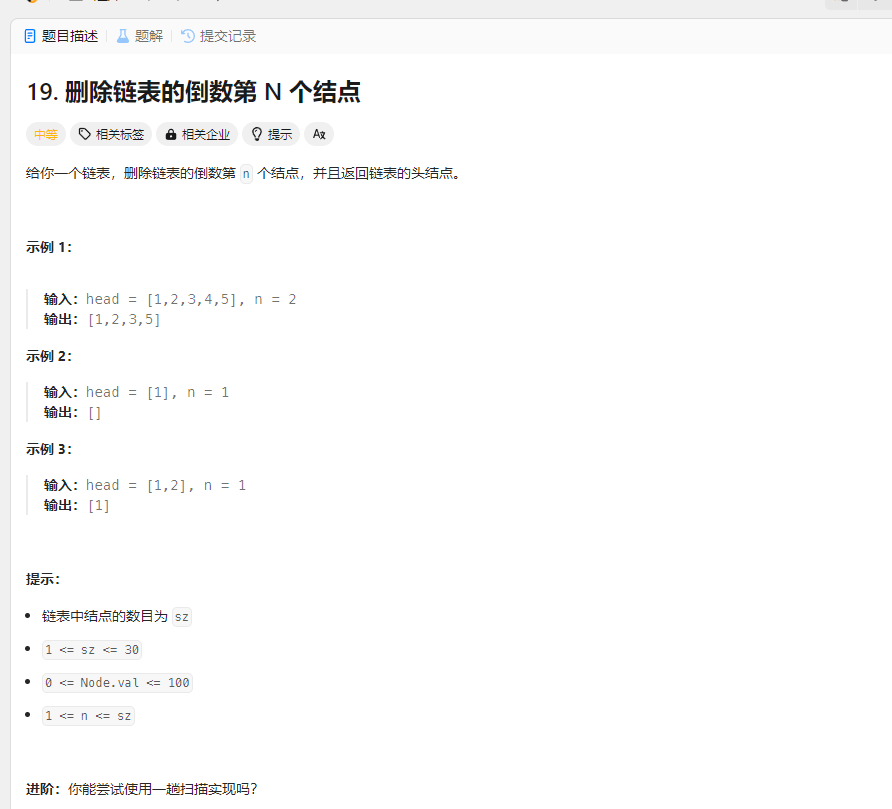
删除链表的倒数第N个节点

题目

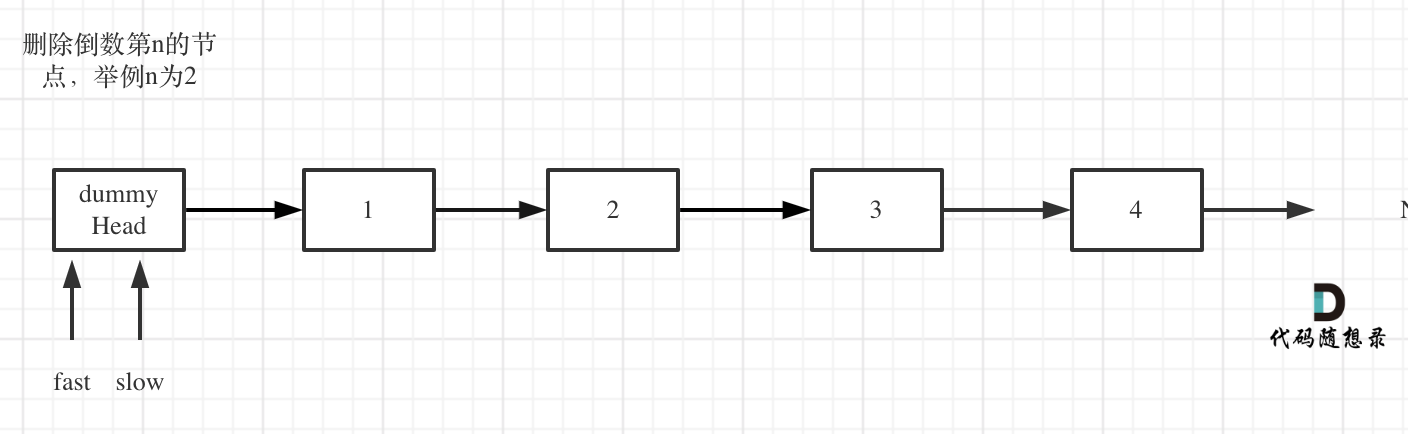
解法：

1.双指针法

双指针的经典应用，如果要删除倒数第n个节点，让fast移动n步，然后让fast和slow同时移动，直到fast指向链表末尾。删掉slow所指向的节点就可以了。

思路是这样的，但要注意一些细节。

分为如下几步：

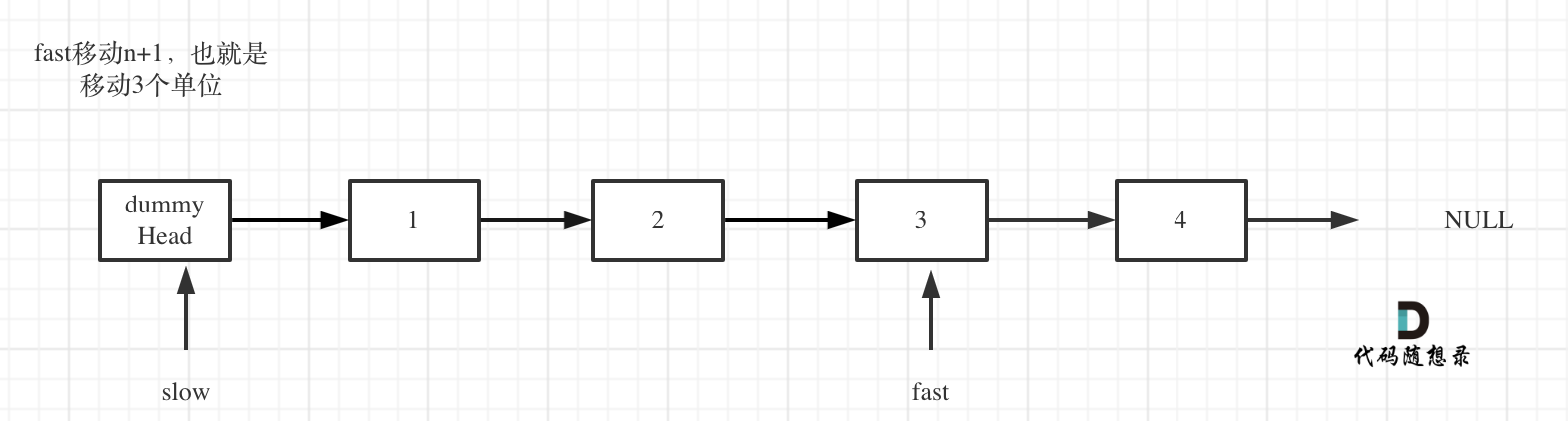
  • fast首先走n + 1步 ，为什么是n+1呢，因为只有这样同时移动的时候slow才能指向删除节点的上一个节点（方便做删除操作），如图：
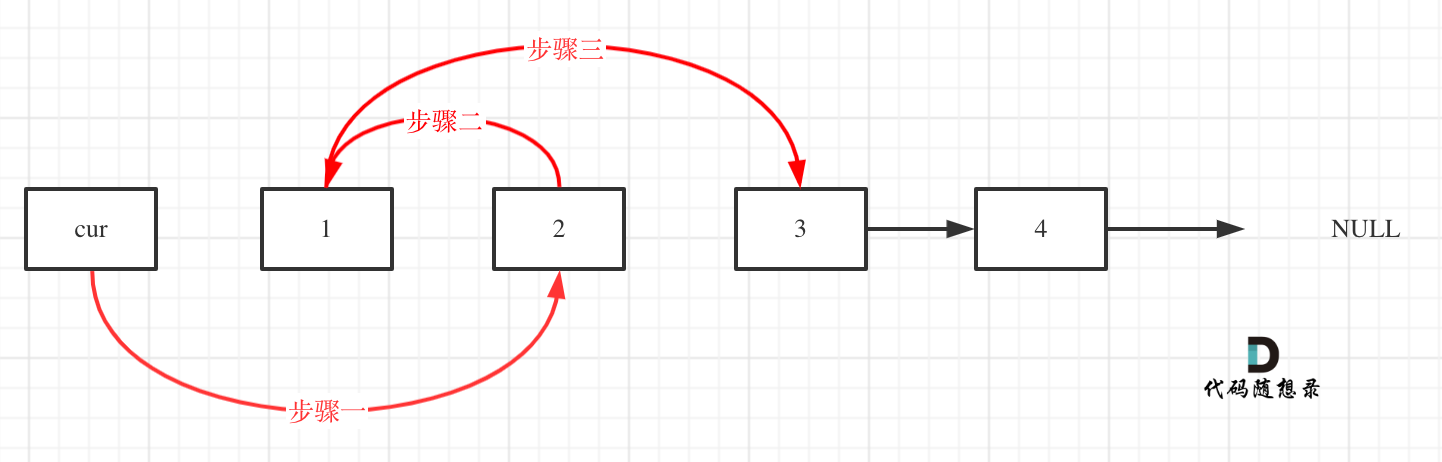
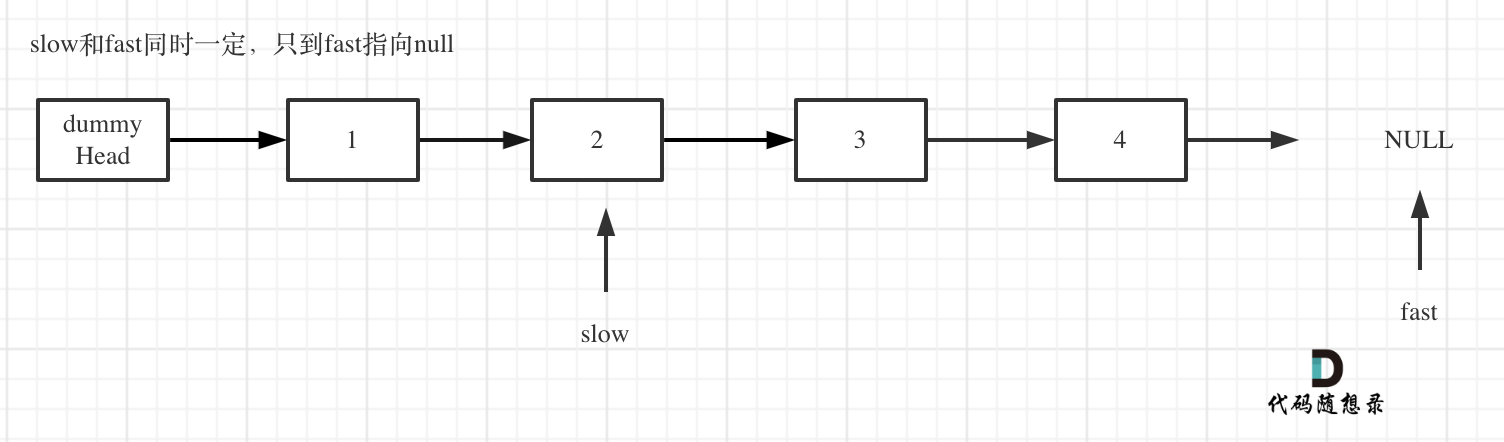
  • fast和slow同时移动，直到fast指向末尾，如题：
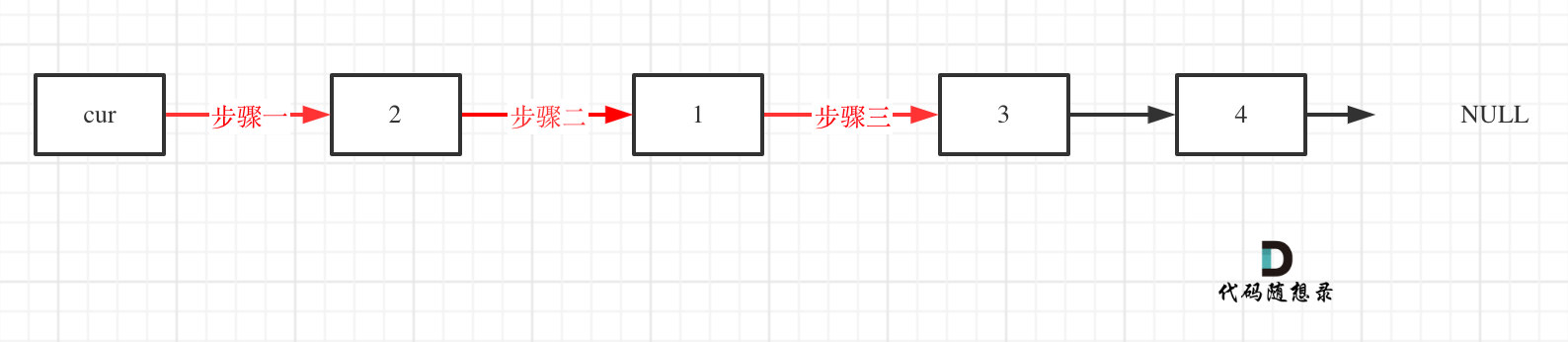
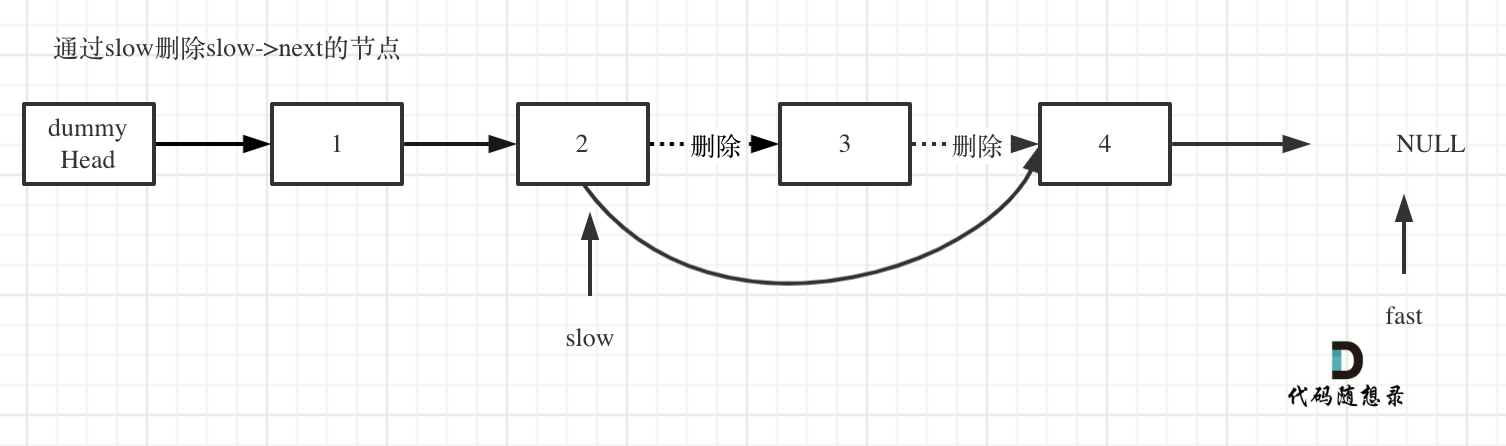
  • 删除slow指向的下一个节点，如图：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
var removeNthFromEnd = function(head, n) {
    let ret = new ListNode(0, head);
    let fast = slow = ret;
    //快指针走n+1步
    for(let i=0;i<=n;i++){
        fast = fast.next;
    }
    while(fast){
        fast = fast.next;
        slow = slow.next;
    }
    slow.next = slow.next.next;

    return ret.next
};

链表相交

题目

解法：

1.快慢双指针法+数学追及问题

可以参考

https://www.programmercarl.com/0142.%E7%8E%AF%E5%BD%A2%E9%93%BE%E8%A1%A8II.html#%E5%85%B6%E4%BB%96%E8%AF%AD%E8%A8%80%E7%89%88%E6%9C%AC

https://www.bilibili.com/video/BV1u341187v3?spm_id_from=333.880.my_history.page.click

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
var getIntersectionNode = function (headA, headB) {
    let cur = headA;
    while (cur && cur.next) {
        cur = cur.next;
    }
    cur.next = headB;

    let fast = slow = headA;

    while (slow && fast && fast.next) {

        fast = fast.next.next;
        slow = slow.next;

        if (!fast) {
            cur.next = null;
            return null;
        }

        if (fast === slow) {
            fast = headA;
            while (fast && slow) {
                if (fast === slow) {
                    cur.next = null;
                    return fast;
                }
                fast = fast.next;
                slow = slow.next;
            }
        }
    }
    cur.next = null;
    return null;
};

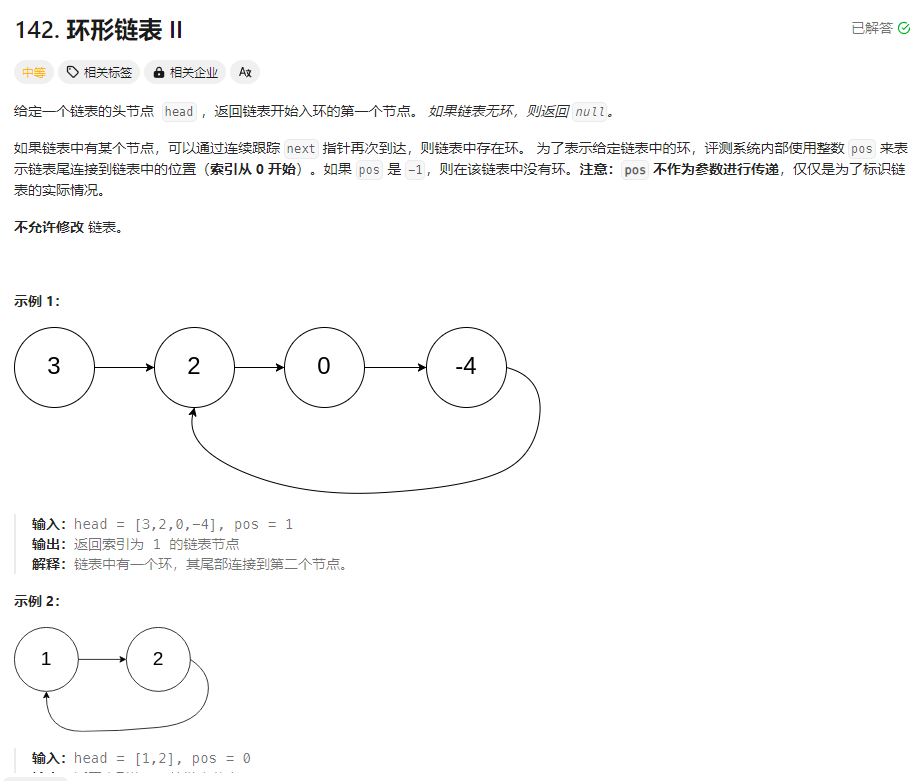
环形链表

题目

解法：

1.快慢双指针法+数学追及问题

https://www.programmercarl.com/0142.%E7%8E%AF%E5%BD%A2%E9%93%BE%E8%A1%A8II.html#%E5%85%B6%E4%BB%96%E8%AF%AD%E8%A8%80%E7%89%88%E6%9C%AC

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
var detectCycle = function(head) {
    if(!head || !head.next) return null;
    let slow =head.next, fast = head.next.next;
    while(fast && fast.next) {
        slow = slow.next;
        fast = fast.next.next;
        if(fast == slow) {
            slow = head;
            while (fast !== slow) {
                slow = slow.next;
                fast = fast.next;
            }
            return slow;
        }
    }
    return null;
};

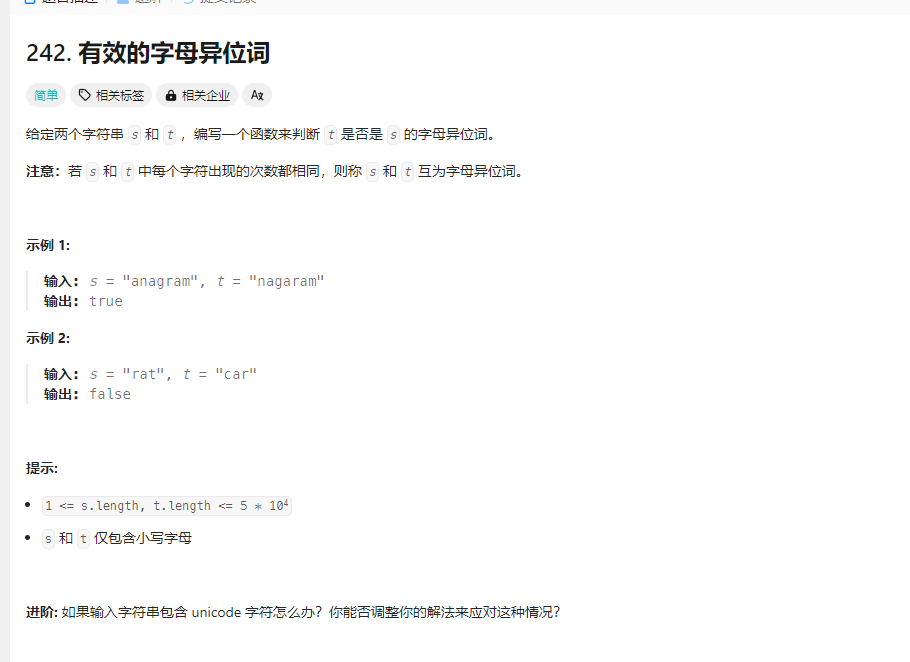
哈希表

有效的字母异位词

题目

解法：

参考

https://www.programmercarl.com/0242.%E6%9C%89%E6%95%88%E7%9A%84%E5%AD%97%E6%AF%8D%E5%BC%82%E4%BD%8D%E8%AF%8D.html#%E5%85%B6%E4%BB%96%E8%AF%AD%E8%A8%80%E7%89%88%E6%9C%AC

1.Map的哈希结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
var isAnagram = function(s, t) {
   if(s.length != t.length){
    return false;
   }
   let map  = new Map(); 
   for(let item of s){
    map.set(item,(map.get(item) || 0)+1);
   }
   for(let item of t){
    if(!map.get(item)){
        return false;
    }
    map.set(item,(map.get(item)-1 || 0))
   }
   return true;
};

两个数组的交集

题目

解法：

1.带有去重的Set哈希结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
var intersection = function(nums1, nums2) {
    // 根据数组大小交换操作的数组
    if(nums1.length < nums2.length) {
        const _ = nums1;
        nums1 = nums2;
        nums2 = _;
    }
    const nums1Set = new Set(nums1);
    const resSet = new Set();
    // for(const n of nums2) {
    //     nums1Set.has(n) && resSet.add(n);
    // }
    // 循环要比迭代器快
    for(let i = nums2.length - 1; i >= 0; i--) {
        nums1Set.has(nums2[i]) && resSet.add(nums2[i]);
    }
    //转化为数组
    return Array.from(resSet);
};

快乐数

题目

解法：

1.带有去重的Set哈希结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
var isHappy = function(n) {
    //求每个位上的数的平方和操作
    let getSum = function(n){
        let sum  = 0;
        while(n>0){
            let digit = n%10;
            sum += (digit*digit);
            n = Math.floor(n/10);
        }
        return sum;
    }

	//Set结构排除无限循环
    let set1 = new Set();
    while(n!=1){
     n = getSum(n);
     if(set1.has(n)){
        return false;
     }
     set1.add(n);
    }
    return true;
};

两数之和

题目

解法：

1.我的解法:两重循环
1
2
3
4
5
6
7
8
9
var twoSum = function(nums, target) {
    for(let i = 0;i<nums.length;i++){
        for(let j = i+1;j<nums.length;j++){
            if(nums[i]+nums[j] == target &&i!=j){
                return [i,j];
            }
        }
    }
};
2.最优解：哈希结构Map
1
2
3
4
5
6
7
8
9
10
11
var twoSum = function (nums, target) {
    const hash = new Map();

    for (let i = 0; i < nums.length; i++) {
        if (hash.has(target - nums[i])) {
            return [i, hash.get(target - nums[i])];
        }
        hash.set(nums[i], i);
    }
};

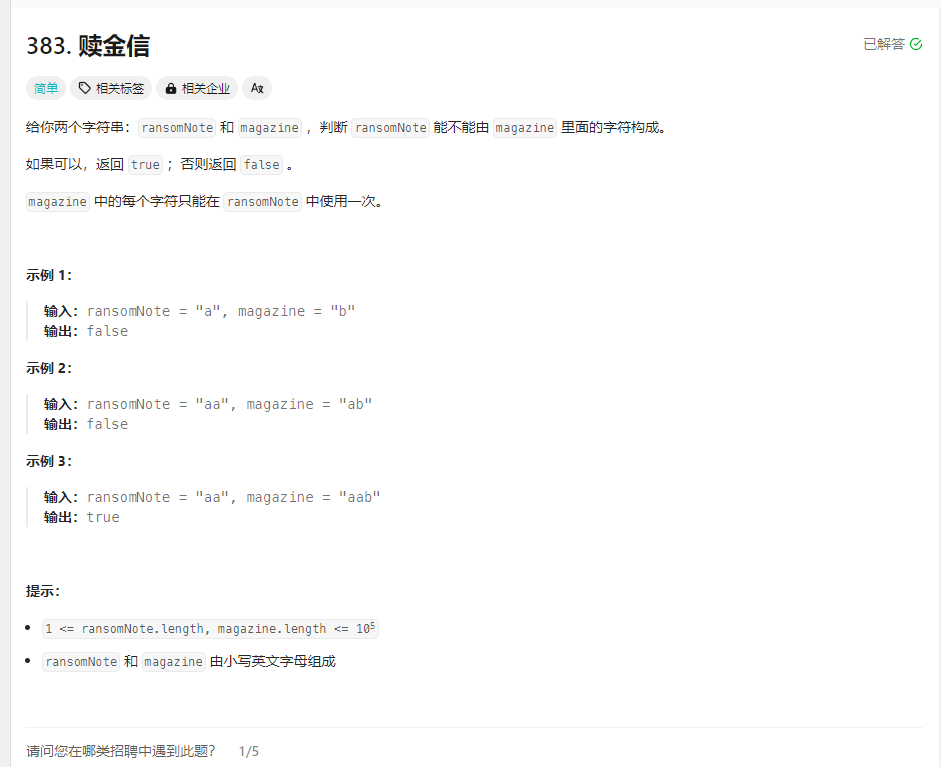
赎金信

题目

解法：

1.数组哈希结构
1
2
3
4
5
6
7
8
9
10
11
12
13
var canConstruct = function(ransomNote, magazine) {
    const strArr = new Array(26).fill(0), 
        base = "a".charCodeAt();
    for(const s of magazine) {  // 记录各个字符出现次数
        strArr[s.charCodeAt() - base]++;
    }
    for(const s of ransomNote) { // 对应的字符个数做-操作
        const index = s.charCodeAt() - base;
        if(!strArr[index]) return false;  // 如果没记录过直接返回false
        strArr[index]--;
    }
    return true;
};

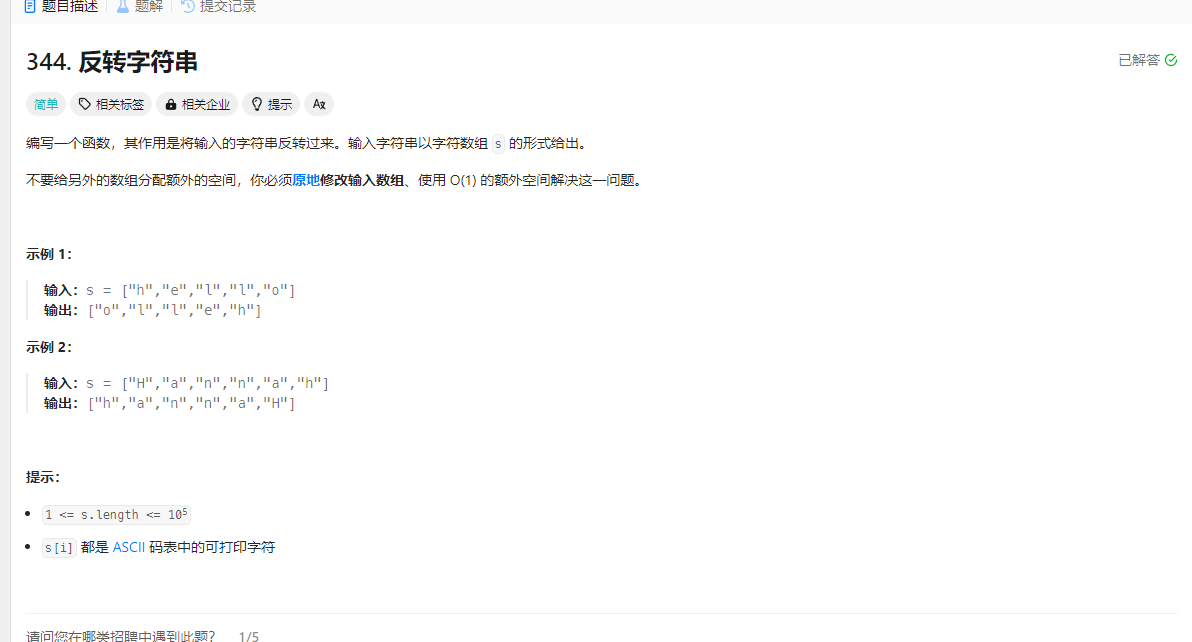
字符串

反转字符串

题目

解法

1.双指针法
1
2
3
4
5
6
7
8
9
10
11
12
var reverseString = function(s) {
    let length  = s.length-1;
    let l = 0,r = length;
    while(l<r){
        let temp = s[l];
        s[l] = s[r];
        s[r] = temp;
        l++;
        r--;
    }
    return s;
};

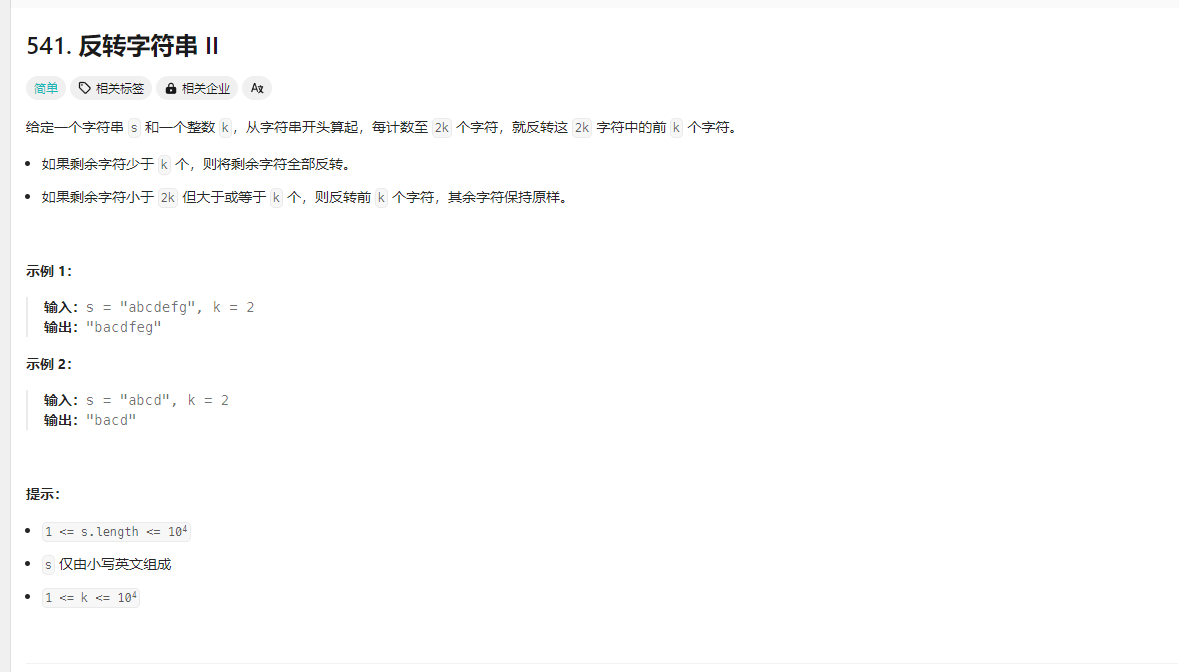
反转字符串进阶

题目

解法

https://www.programmercarl.com/0541.%E5%8F%8D%E8%BD%AC%E5%AD%97%E7%AC%A6%E4%B8%B2II.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE

1.普通分类处理
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
const reverse = (arr, left, right) => {
    while (left < right) {
        const temp = arr[left];
        arr[left] = arr[right];
        arr[right] = temp;
        left++;
        right--;
    }
}



var reverseStr = function (s, k) {
    let n = s.length;
    let arr =  Array.from(s);
    for(let i = 0;i<n;i+= 2*k){
        reverse(arr,i,Math.min(i+k,n)-1);
    }

    return arr.join('');
};

2.我的错误解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
let l = 0, r = s.length - 1;
  let temp;
  for (let i = 0; i < s.length; i += 2 * k) {
      r = Math.floor(i/2) - 1;
      while (l < r) {
          temp = s[l];
          s[l] = s[r];
          s[r] = temp;
          l++;
          r--;
      }
      l = i + 1;
      //如果剩余字符小于 2k 但大于或等于 k 个，则反转前 k 个字符，其余字符保持原样。
      if (i + k < s.length && i + 2*k > s.length) {
          l = i - 1;
          r = i + k - 1;
          while (l < r) {
              temp = s[l];
              s[l] = s[r];
              s[r] = temp;
              l++;
              r--;
          }
      }else if(i + k > s.length) {
          l = i - 1;
          r = s.length - 1
          while (l < r) {
              temp = s[l];
              s[l] = s[r];
              s[r] = temp;
              l++;
              r--;
          }
      }
  }
  return s

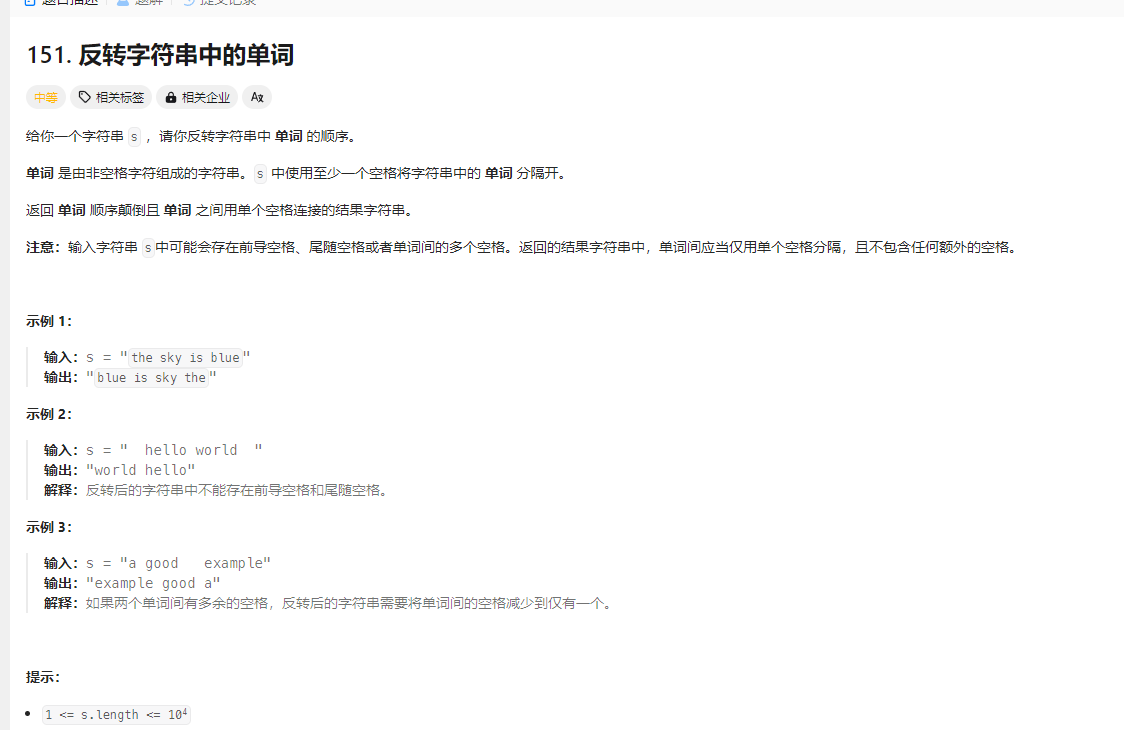
反转字符串中的单词

题目

解法

https://www.programmercarl.com/0151.%E7%BF%BB%E8%BD%AC%E5%AD%97%E7%AC%A6%E4%B8%B2%E9%87%8C%E7%9A%84%E5%8D%95%E8%AF%8D.html#%E5%85%B6%E4%BB%96%E8%AF%AD%E8%A8%80%E7%89%88%E6%9C%AC

1.双指针法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
var reverseWords = function (s) {
    //字符串转数组
    const strArr = Array.from(s);
    //移除多余空格
    removeSpace(strArr);
    //翻转整个字符串
    reverse(strArr, 0, strArr.length - 1);
    let start = 0;

    for (let i = 0; i <= strArr.length; i++) {
        if (strArr[i] === ' ' || i === strArr.length) {
            // 翻转单词

            reverse(strArr, start, i - 1);

            start = i + 1;
        }
    }
    return strArr.join('');
};


function removeExtraSpaces(strArr) {
    let slowIndex = 0;
    let fastIndex = 0;

    while (fastIndex < strArr.length) {
        // 移除开始位置和重复的空格
        if (strArr[fastIndex] === ' ' && (fastIndex === 0 || strArr[fastIndex - 1] === ' ')) {
            fastIndex++;
        } else {
            strArr[slowIndex++] = strArr[fastIndex++];
        }
    }

    // 移除末尾空格
    strArr.length = strArr[slowIndex - 1] === ' ' ? slowIndex - 1 : slowIndex;
}

var removeSpace = function (s) {
    let slow = fast = 0;
    while (fast < s.length) {
        //移除开头空格和重复的空格
        if (s[fast] == ' ' && (fast == 0 || s[fast - 1] == ' ')) {
            fast++;
        } else {
            s[slow] = s[fast];
            fast++;
            slow++;
        }
        //没有遇到需要处理的空格,快慢指针向前

    }
    //移除末尾空格，直接截取长度，排除末尾空格，这里找bug找了半小时，因为这个判断length长度要在上面这个循环遍历结束后才进行
    if (s[slow - 1] == ' ') {
        s.length = slow - 1;
    } else {
        s.length = slow;
    }
}

//反转字符串
var reverse = function (s, start, end) {
    let l = start, r = end;
    while (l < r) {
        let temp = s[l];
        s[l] = s[r];
        s[r] = temp;
        l++;
        r--;
    }
}

栈和队列

用栈实现队列

题目

解法：

1.入栈和出栈
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
// 使用两个数组的栈方法（push, pop） 实现队列
/**
* Initialize your data structure here.
*/
var MyQueue = function() {
   this.stackIn = [];
   this.stackOut = [];
};

/**
* Push element x to the back of queue. 
* @param {number} x
* @return {void}
*/
MyQueue.prototype.push = function(x) {
   this.stackIn.push(x);
};

/**
* Removes the element from in front of queue and returns that element.
* @return {number}
*/
MyQueue.prototype.pop = function() {
   const size = this.stackOut.length;
   if(size) {
       return this.stackOut.pop();
   }
   while(this.stackIn.length) {
       this.stackOut.push(this.stackIn.pop());
   }
   return this.stackOut.pop();
};

/**
* Get the front element.
* @return {number}
*/
MyQueue.prototype.peek = function() {
   const x = this.pop();
   this.stackOut.push(x);
   return x;
};

/**
* Returns whether the queue is empty.
* @return {boolean}
*/
MyQueue.prototype.empty = function() {
   return !this.stackIn.length && !this.stackOut.length
};

用队列实现栈

题目

解法：

1.单个队列实现

使用数组（push, shift）模拟队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

var MyStack = function() {
    this.queue = [];
};

/** 
 * @param {number} x
 * @return {void}
 */
MyStack.prototype.push = function(x) {
    this.queue.push(x);
};

/**
 * @return {number}
 */
//这里相当于循环队列操作，把除了队列里最后一个元素外其它元素移到队列尾
MyStack.prototype.pop = function() {
    let size = this.queue.length;
    while(size>1){
        this.queue.push(this.queue.shift());
        size--;
    }
    return this.queue.shift();
};

/**
 * @return {number}
 */
//调用这个实现的pop方法，防止影响真的弹出，所以又进队列原先是1234 ，pop后为4123->123，再恢复1234
MyStack.prototype.top = function() {
    let x = this.pop();
    this.queue.push(x);
    return x;
};

/**
 * @return {boolean}
 */
MyStack.prototype.empty = function() {
    if(!this.queue.length){
        return true;
    }else{
        return false;
    }
};

/**
 * Your MyStack object will be instantiated and called as such:
 * var obj = new MyStack()
 * obj.push(x)
 * var param_2 = obj.pop()
 * var param_3 = obj.top()
 * var param_4 = obj.empty()
 */

最小栈

题目

解法：

1.辅助栈

https://leetcode.cn/problems/min-stack/solutions/242190/zui-xiao-zhan-by-leetcode-solution/?envType=study-plan-v2&envId=selected-coding-interview

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
var MinStack = function() {
    this.x_stack = [];
    this.min_stack = [Infinity];
};

MinStack.prototype.push = function(x) {
    this.x_stack.push(x);
    this.min_stack.push(Math.min(this.min_stack[this.min_stack.length - 1], x));
};

MinStack.prototype.pop = function() {
    this.x_stack.pop();
    this.min_stack.pop();
};

MinStack.prototype.top = function() {
    return this.x_stack[this.x_stack.length - 1];
};

MinStack.prototype.getMin = function() {
    return this.min_stack[this.min_stack.length - 1];
};


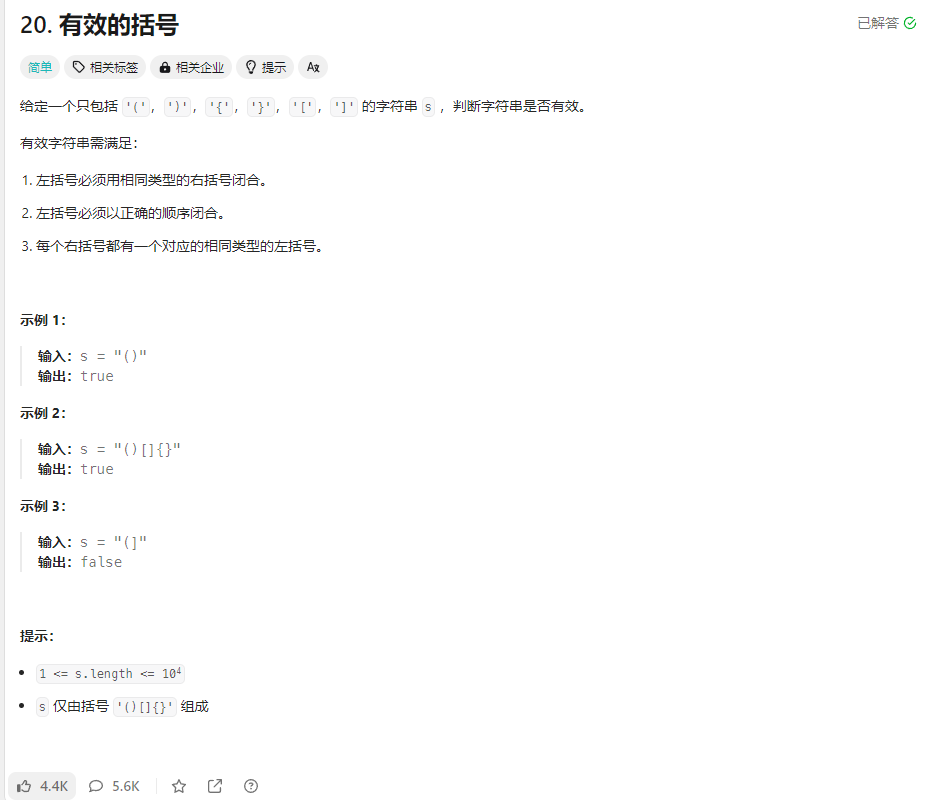
有效的括号

题目

解法：

1.栈解法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
var isValid = function (s) {
    const stack = [];
    for (let i = 0; i < s.length; i++) {
        const c = s[i];
        if(c=='('){
            stack.push(')');
        }else if(c=='{'){
            stack.push('}');
        }else if(c=='['){
            stack.push(']');
        }else if(c!=stack.pop()){
            return false;
        }
        
    }
    return stack.length === 0

};

删除字符串中的所有相邻重复项

题目

解法：

1.栈解法

用数组模拟栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 * @param {string} s
 * @return {string}
 */
var removeDuplicates = function(s) {
    let stack = [];
    for(const i of s){
        if(i  == stack[stack.length-1]){
            stack.pop();
        }else{
            stack.push(i);
        }
    }
    return stack.join('')
    
};
数组的pop()和push();

在尾部追加，类似于压栈，原数组会变。

1
2
3
const arr = [1, 2, 3]
arr.push(8)
console.log(arr) // [1, 2, 3, 8]

在尾部弹出，类似于出栈，原数组会变。数组的 push & pop 可以模拟常见数据结构之一：栈。

1
2
3
4
5
6
7
8
9
10
11
12
13
const arr = [1, 2, 3]
const popVal = arr.pop()
console.log(popVal) // 3
console.log(arr) // [1, 2]

// 数组模拟常见数据结构之一：栈
const stack = [0, 1]
stack.push(2) // 压栈
console.log(stack) // [0, 1, 2]

const popValue = stack.pop() // 出栈
console.log(popValue) // 2
console.log(stack) // [0, 1]

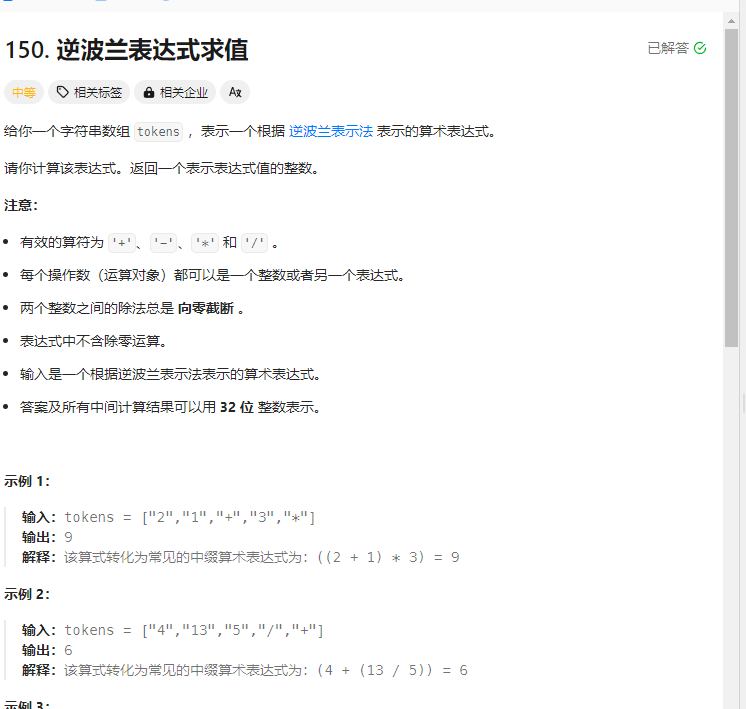
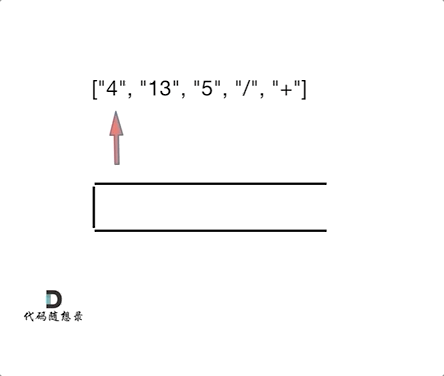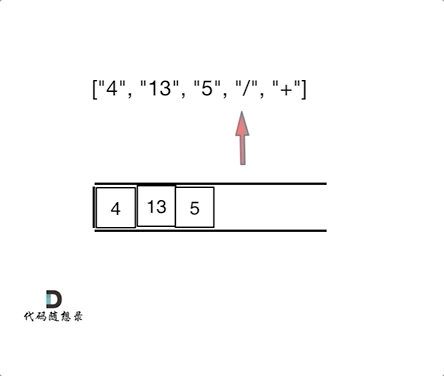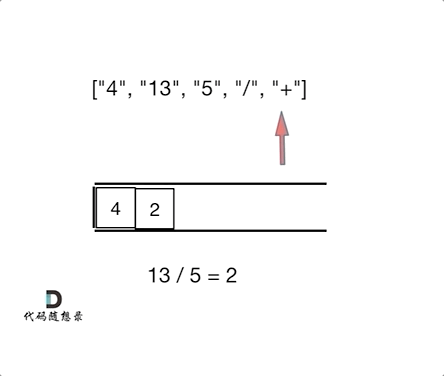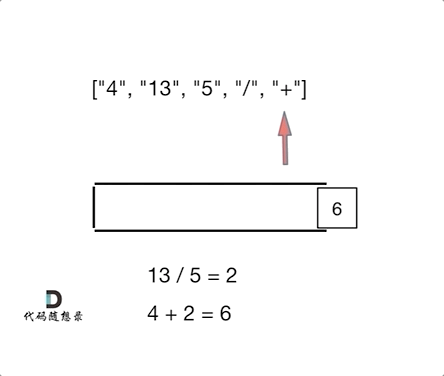
逆波兰表达式求值

题目

解法：

1.栈解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * @param {string[]} tokens
 * @return {number}
 */
//字符串数组
var evalRPN = function (tokens) {
    //数组模拟栈
    const stack = [];
    //遍历操作
    for (let i of tokens) {
        if (!isNaN(Number(i))) {
            stack.push(i);
        } else {
            //表达式操作
            //因为要考虑被除数和除数的情况，所以要赋值操作方便
            const b = stack.pop();
            const a = stack.pop();
            switch (i) {
                case '+':
                    //因为是字符串数组+会出现错误，要转换为数字类型
                    stack.push(Number(a) + Number(b));
                    break;
                case '-':
                    stack.push(a - b);
                    break;
                case '*':
                    stack.push(a * b);
                    break;
                case '/':
                    //考虑0的情况
                    stack.push(a / b | 0 );
                    break;
            }
        }
    }
    return stack[0]; // 因没有遇到运算符而待在栈中的结果
};

逆波兰表达式主要有以下两个优点：

  • 去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
  • 适合用栈操作运算：遇到数字则入栈；遇到运算符则取出栈顶两个数字进行计算，并将结果压入栈中。

前 K 个高频元素

题目

解法：

这道题目主要涉及到如下三块内容：

  1. 要统计元素出现频率
  2. 对频率排序
  3. 找出前K个高频元素

首先统计元素出现的频率，这一类的问题可以使用map来进行统计。

缺省情况下priority_queue利用max-heap（大顶堆）完成对元素的排序，这个大顶堆是以vector为表现形式的complete binary tree（完全二叉树）。

什么是堆呢？

堆是一棵完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。 如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆。

所以大家经常说的大顶堆（堆头是最大元素），小顶堆（堆头是最小元素），如果懒得自己实现的话，就直接用priority_queue（优先级队列）就可以了，底层实现都是一样的，从小到大排就是小顶堆，从大到小排就是大顶堆。

本题我们就要使用优先级队列来对部分频率进行排序。

为什么不用快排呢， 使用快排要将map转换为vector的结构，然后对整个数组进行排序， 而这种场景下，我们其实只需要维护k个有序的序列就可以了，所以使用优先级队列是最优的。

此时要思考一下，是使用小顶堆呢，还是大顶堆？

有的同学一想，题目要求前 K 个高频元素，那么果断用大顶堆啊。

那么问题来了，定义一个大小为k的大顶堆，在每次移动更新大顶堆的时候，每次弹出都把最大的元素弹出去了，那么怎么保留下来前K个高频元素呢。

而且使用大顶堆就要把所有元素都进行排序，那能不能只排序k个元素呢？

所以我们要用小顶堆，因为要统计最大前k个元素，只有小顶堆每次将最小的元素弹出，最后小顶堆里积累的才是前k个最大元素。

1.小顶堆+栈解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
// js 没有堆 需要自己构造
class Heap {
    constructor(compareFn) {
        this.compareFn = compareFn;
        this.queue = [];
    }

    // 添加
    push(item) {
        // 推入元素
        this.queue.push(item);

        // 上浮
        let index = this.size() - 1; // 记录推入元素下标
        let parent = Math.floor((index - 1) / 2); // 记录父节点下标

        while (parent >= 0 && this.compare(parent, index) > 0) { // 注意compare参数顺序
            [this.queue[index], this.queue[parent]] = [this.queue[parent], this.queue[index]];

            // 更新下标
            index = parent;
            parent = Math.floor((index - 1) / 2);
        }
    }

    // 获取堆顶元素并移除
    pop() {
        // 堆顶元素
        const out = this.queue[0];

        // 移除堆顶元素 填入最后一个元素
        this.queue[0] = this.queue.pop();

        // 下沉
        let index = 0; // 记录下沉元素下标
        let left = 1; // left 是左子节点下标 left + 1 则是右子节点下标
        let searchChild = this.compare(left, left + 1) > 0 ? left + 1 : left;

        while (searchChild !== undefined && this.compare(index, searchChild) > 0) { // 注意compare参数顺序
            [this.queue[index], this.queue[searchChild]] = [this.queue[searchChild], this.queue[index]];

            // 更新下标
            index = searchChild;
            left = 2 * index + 1;
            searchChild = this.compare(left, left + 1) > 0 ? left + 1 : left;
        }

        return out;
    }

    size() {
        return this.queue.length;
    }

    // 使用传入的 compareFn 比较两个位置的元素
    compare(index1, index2) {
        // 处理下标越界问题
        if (this.queue[index1] === undefined) return 1;
        if (this.queue[index2] === undefined) return -1;

        return this.compareFn(this.queue[index1], this.queue[index2]);
    }

}

const topKFrequent = function (nums, k) {
    const map = new Map();

    for (const num of nums) {
        map.set(num, (map.get(num) || 0) + 1);
    }

    // 创建小顶堆
    const heap= new Heap((a, b) => a[1] - b[1]);

    // entry 是一个长度为2的数组，0位置存储key，1位置存储value
    for (const entry of map.entries()) {
        heap.push(entry);

        if (heap.size() > k) {
            heap.pop();
        }
    }

    // return heap.queue.map(e => e[0]);

    const res = [];

    for (let i = heap.size() - 1; i >= 0; i--) {
        res[i] = heap.pop()[0];
    }

    return res;
};

二叉树

先序遍历、中序遍历、后序遍历(递归)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
/**
先序遍历
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var preorderTraversal = function(root) {
    let a = [];
    const dfs = function(node){
        if(node == null){
            return;
        }
        a.push(node.val);
        dfs(node.left);
        dfs(node.right);
    }
    dfs(root);
    return a;
};



/**中序遍历
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var inorderTraversal = function(root) {
    let a = [];
    const dfs = function(node){
        if(node == null){
            return;
        }
        dfs(node.left);
        a.push(node.val);
        dfs(node.right);
    }
    dfs(root);
    return a;
};


/**后序遍历
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var postorderTraversal = function(root) {
    let a = [];
    const dfs = function(node){
        if(node == null){
            return;
        }
        dfs(node.left);
        dfs(node.right);
        a.push(node.val);
    }
    dfs(root);
    return a;
};

先序遍历、中序遍历、后序遍历(非递归)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97

var preorderTraversal = function (root) {
    //保存栈
    let a = [root];
    //结果栈
    let b = []
    //空树的情况
    if (!root) {
        return b;
    }
    //非空树
    while(a.length){
         //这个指针head很重要，不能固定，而是要随着出栈的元素变化
        let head = a.pop();
         //保存栈出，那么结果栈就得进
        b.push(head.val);
         //如果有右树，进保存栈
        if(head.right){
            a.push(head.right);
        }
        //如果有左树，进保存栈
        if(head.left){
            a.push(head.left);
        }
    }
    return b;
};





var inorderTraversal = function (root) {
    //保存栈
    let b = [];
    //结果栈
    let res = [];
    //处理空树的情况
    if (root == null) {
        return res;
    }
    //先让临时变量指向根节点
    let head = root;
    //当保存栈不为空 或 临时变量有意义时
    while (b.length || head) {
        //遍历左子树节点进保存栈
        if (head != null) {
            b.push(head);
            head = head.left;
        }else{
            //遍历左结束，开始出栈左和中
            head = b.pop();
            //保存栈出，那么结果栈就得进
            res.push(head.val);

            //遍历右子树重复  遍历左子树节点进保存栈的操作
            //出栈右
            head = head.right;
        }
    };
    return res;
}







var postorderTraversal = function(root) {
    //结果栈
    let res = [];
    //保存栈
    let b = [root];
    //空树的情况
    if(root == null){
        return res;
    }
    //非空树
    while(b.length){
        //这个指针head很重要，不能固定，而是要随着出栈的元素变化
        let head = b.pop();
        //保存栈出，那么结果栈就得进
        res.push(head.val);
        //如果有左树，进保存栈
        if(head.left){
           b.push(head.left)
        }
        //如果有右树，进保存栈
        if(head.right){
           b.push(head.right)
        }

    }
    //反转结果栈
    return res.reverse();
};

二叉树的统一迭代法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
// 前序遍历：中左右
// 压栈顺序：右左中

var preorderTraversal = function(root, res = []) {
    const stack = [];
    if (root) stack.push(root);
    while(stack.length) {
        const node = stack.pop();
        if(!node) {
            res.push(stack.pop().val);
            continue;
        }
        if (node.right) stack.push(node.right); // 右
        if (node.left) stack.push(node.left); // 左
        stack.push(node); // 中
        stack.push(null);
    };
    return res;
};


//  中序遍历：左中右
//  压栈顺序：右中左
 
var inorderTraversal = function(root, res = []) {
    const stack = [];
    if (root) stack.push(root);
    while(stack.length) {
        const node = stack.pop();
        if(!node) {
            res.push(stack.pop().val);
            continue;
        }
        if (node.right) stack.push(node.right); // 右
        stack.push(node); // 中
        stack.push(null);
        if (node.left) stack.push(node.left); // 左
    };
    return res;
};


// 后续遍历：左右中
// 压栈顺序：中右左
 
var postorderTraversal = function(root, res = []) {
    const stack = [];
    if (root) stack.push(root);
    while(stack.length) {
        const node = stack.pop();
        if(!node) {
            res.push(stack.pop().val);
            continue;
        }
        stack.push(node); // 中
        stack.push(null);
        if (node.right) stack.push(node.right); // 右
        if (node.left) stack.push(node.left); // 左
    };
    return res;
};

层序遍历

题目

解法：

1.队列模拟
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
var levelOrder = function(root) {
    let queue = [];
    let outqueue = []
    if(root){
        queue.push(root);
    }
    while(queue.length > 0){
        let temp = queue.length;
        let tempqueue  = [];
        for(let i = 0;i<temp;i++){
            let out = queue.shift();
            tempqueue.push(out.val)
            if(out.left){
                queue.push(out.left);
            }
            if(out.right){
                queue.push(out.right);
            }
        }
        outqueue.push(tempqueue);
    }
    return outqueue;
};

翻转二叉树

题目

解法：

1.层序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
//使用层序遍历反转二叉树
var invertTree = function(root) {
    //队列保存节点
    let queue = [];
    //如果不为空树，根节点进队
    if(root!=null){
        queue.push(root);
    }
    //当队列不为空时
    while(queue.length>0){
        let out = queue.pop();
        //交换左右子节点
        let temp = out.left;
        out.left = out.right;
        out.right = temp;

        //下一层加入
        if(out.left){
            queue.push(out.left);
        }
        if(out.right){
            queue.push(out.right);
        }
    }
    return root;
};
2.先序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

//先序遍历反转二叉树
var invertTree = function(root) {
    let stack = [];
    if(root!=null){
        stack.push(root);
    }
    while(stack.length>0){
        let head = stack.pop();
        let temp = head.left;
        head.left = head.right;
        head.right = temp;

        if(head.right){
            stack.push(head.right);
        }
        if(head.left){
            stack.push(head.left);
        }
    }
    return root
};
3.递归遍历
1
2
3
4
5
6
7
8
9
10
11
12
13

var invertTree = function(root) {
    // 终止条件
    if (!root) {
        return null;
    }
    // 交换左右节点
    //相当于swap的过程，只不过这两个节点还要各自在递归下去
    const rightNode = root.right;
    root.right = invertTree(root.left);
    root.left = invertTree(rightNode);
    return root;
};

N叉树的前序遍历

题目

解法：

1.递归法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * // Definition for a Node.
 * function Node(val, children) {
 *    this.val = val;
 *    this.children = children;
 * };
 */

/**
 * @param {Node|null} root
 * @return {number[]}
 */
var preorder = function (root) {
    let res = [];
    const dfs = function (root) {
        if (root == null) {
            return;
        }
        let head = root;
        res.push(head.val);//1
        for (child of head.children) {//324
            dfs(child);//56
        }


    }
    dfs(root);
    return res;
};

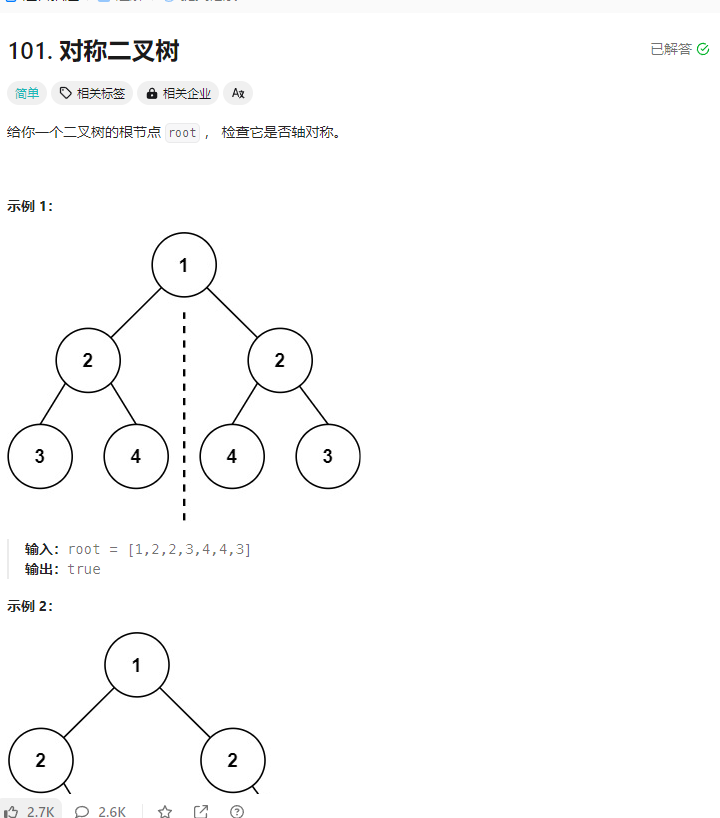
对称二叉树

题目

解法：

1.分类讨论
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
//递归法

var compare = function(node1,node2){
    //分类讨论
    if(node1 == null && node2 == null){
            return true;
        }
    else if(node1 == null && node2 != null){
        return false;
    }else if(node1 != null && node2 == null){
        return false;
    }else if(node1.val!= node2.val){
        return false;
    }else{
        //递归左右的镜像
       return compare(node1.left,node2.right) && compare(node1.right,node2.left);
    }
}




var isSymmetric = function(root) {
    if(root == null){
        return true;
    }
    //返回递归结果
    return compare(root.left,root.right);

};

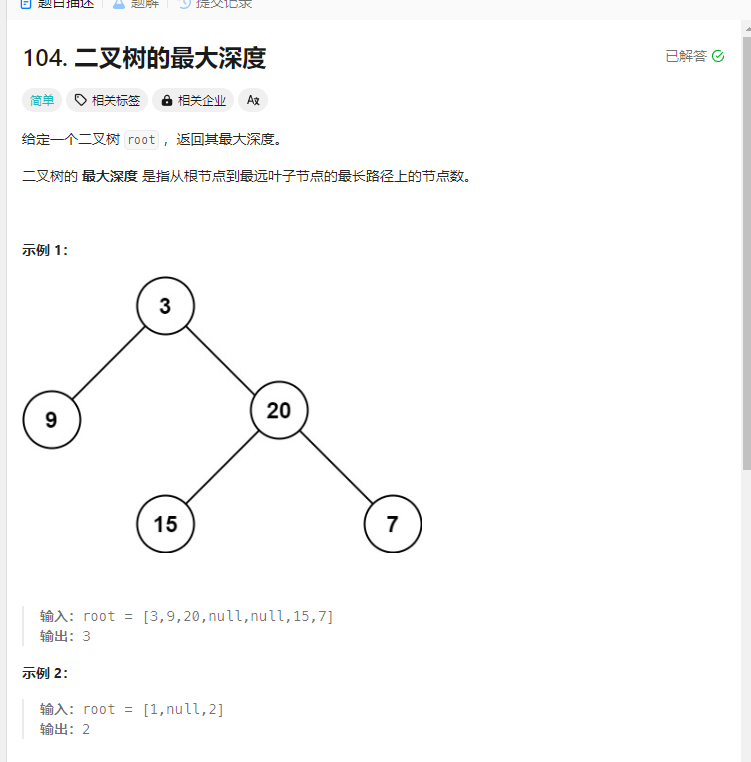
二叉树的最大深度

题目

解法：

1.层次遍历迭代法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function(root) {
    //层次遍历二叉树求最大深度
    let maxlength = 0;
    let queue = [];
    if(root == null){
        return 0;
    }
    if(root!= null){
        queue.push(root);
    }
    while(queue.length>0){
        //要用临时变量存储每一层的节点数量，防止length随着shift而变化
        let length = queue.length;
        for(let i =0;i<length;i++){
        let temp = queue.shift();
        if(temp.left){
            queue.push(temp.left);
        }
        if(temp.right){
            queue.push(temp.right)
        }
    }
      maxlength += 1;
    }

    return maxlength;
    
};
2.后序递归法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
var maxdepth = function(root) {
    //使用递归的方法 递归三部曲
    //1. 确定递归函数的参数和返回值
    const getdepth = function(node) {
    //2. 确定终止条件
        if(node === null) {
            return 0;
        }
    //3. 确定单层逻辑
        let leftdepth = getdepth(node.left); //左
        let rightdepth = getdepth(node.right); //右
        let depth = 1 + Math.max(leftdepth, rightdepth); //中
        return depth;
    }
    return getdepth(root);
};
3.前序递归法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
var maxDepth = function(root) {
    // 使用递归的方法 递归三部曲
    // 1. 确定递归函数的参数和返回值
    const getdepth = function(node) {
        // 2. 确定终止条件
        if (node === null) {
            return 0;
        }
        // 3. 确定单层逻辑
        let depth = 1; //中
        let leftdepth = getdepth(node.left);//左
        let rightdepth = getdepth(node.right);//右
        depth += Math.max(leftdepth, rightdepth);
        return depth;
    }
    return getdepth(root);
};

前序遍历充分表现出求深度回溯的过程

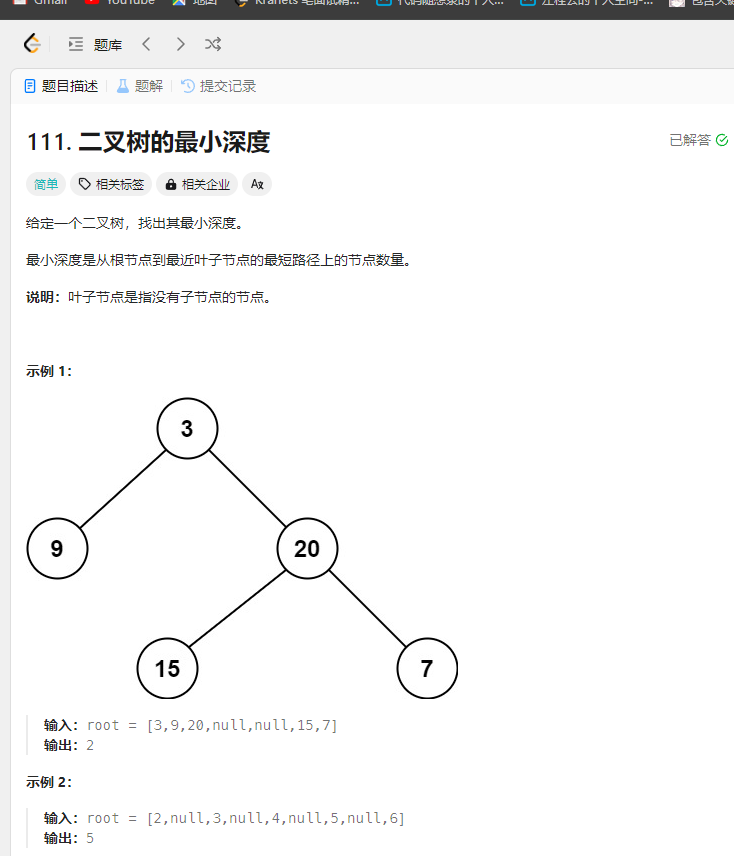
二叉树的最小深度

题目

解法：

1.层次遍历迭代法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var minDepth = function(root) {
    //层次遍历二叉树求最小深度
    let minlength = 1;
    let queue = [];
    if(root == null){
        return 0;
    }
    if(root!= null){
        queue.push(root);
    }
    while(queue.length>0){
        let length = queue.length;
        for(let i =0;i<length;i++){
        let temp = queue.shift();
        //直接返回最小长度
        if(!temp.left && !temp.right){
           return minlength;
        }
        if(temp.left){
            queue.push(temp.left);
        }
        if(temp.right){
            queue.push(temp.right)
        }
    }
    //说明这一层没有叶子节点，所以要层数+1
      minlength += 1;
    }

    return minlength;
    
};

完全二叉树的节点个数

题目

解法：

1.层次遍历法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
// 层次遍历法
var countNodes = function(root) {
    let queue = [];
    let count = 0;
    if(root == null){
        return 0;
    }
    queue.push(root);
    while(queue.length>0){
        let length = queue.length;
        for(let i = 0;i<length;i++){
            let temp = queue.shift();
            count += 1;
            if(temp.left!=null){
                queue.push(temp.left);
            } 
            if(temp.right!=null){
                queue.push(temp.right)
            }
        }
    }
    return count;
};




//递归法
var countNodes = function(root) {
    let getcount = function(node){
        if(node == null){
            return 0;
        }
        let leftnum = getcount(node.left);
        let rightnum = getcount(node.right);
        let treenum = leftnum + rightnum + 1;
        return treenum;
    }

     return getcount(root);
};

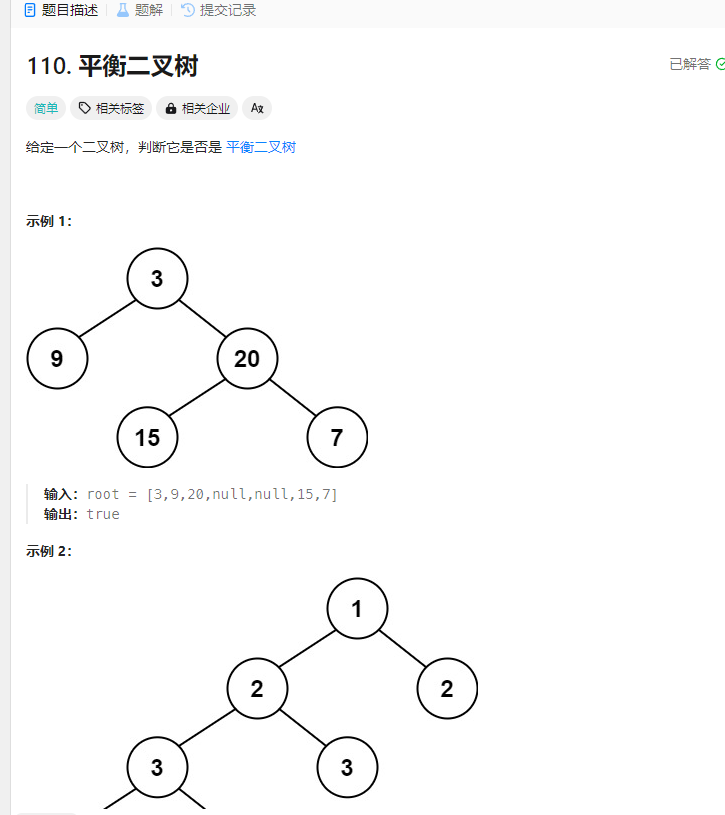
2.递归法

平衡二叉树

题目

解法：

1.后序递归法

求高度 – 后序

求深度 –先序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {boolean}
 */
var isBalanced = function(root) {
    let getheight = function(node){
        //递归出口
        if(node == null){
            return 0;
        }
        // 如果左子树不为平衡二叉树，就直接返回-1  ----左
        let leftHeight = getheight(node.left);
        if(leftHeight == -1){
            return -1;
        }
        // 如果右子树不为平衡二叉树，就直接返回-1 -----右
        let rightHeight = getheight(node.right);
        if(rightHeight == -1){
            return -1;
        }
        // 如果该左右子树高度之差，也就是后序遍历左右中的中节点----中
        // 不为平衡二叉树，就直接返回-1
        if(Math.abs(leftHeight-rightHeight)>1){
            return -1;
        }else{
            return 1 + Math.max(leftHeight,rightHeight);
        }
    }


    return !(getheight(root) === -1)
};

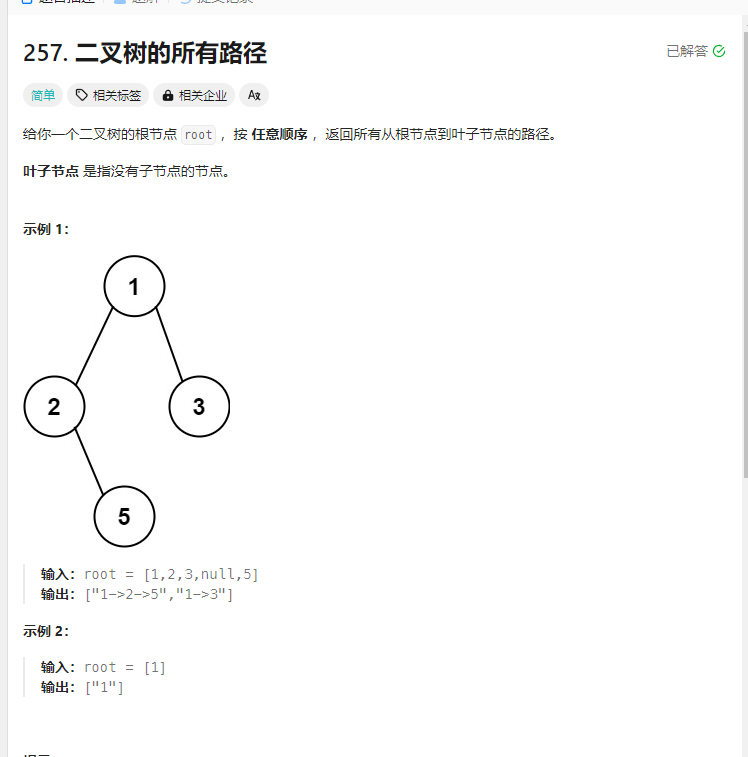
二叉树的所有路径

题目

解法：

1.递归+回溯法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {string[]}
 */
var binaryTreePaths = function(root) {
    let res = [];
    let getPath = function(node,curPath){
        if(node.left == null && node.right == null){
            curPath += node.val;
            res.push(curPath);
            return;
        }
        curPath += node.val +'->';
        if(node.left){
            getPath(node.left,curPath);
        }
        if(node.right){
            getPath(node.right,curPath);
        }
    }
     getPath(root,'');
     return res;
};

https://www.bilibili.com/video/BV1ZG411G7Dh/?vd_source=1d570edaa4d98b311404ac363e136ee7

在给定的 JavaScript 代码中，回溯(backtracking)并不是显式地呈现出来，但实际上在递归过程中确实有回溯的概念。回溯是一种在解决问题时以试错的方式探索所有可能的解空间的方法，当发现当前路径不满足问题要求时，会回退到之前的状态，尝试其他路径。

在这个特定的例子中，回溯体现在函数 getPath 中的递归调用过程中。当递归调用 getPath 函数时，会传递当前节点的左子树或右子树，并且在每一次递归调用之后，都会将路径 curPath 恢复到之前的状态，这就是回溯的体现。

具体来说，在递归调用之前，curPath 会添加当前节点的值和连接符 ->，然后递归调用左右子树，但在递归调用结束后，curPath 并没有改变，而是保持在之前的状态。这样，当递归回到上一层时，curPath 就回到了之前的状态，相当于回退了一个步骤，这就是回溯的过程。

回溯虽然没有显式地写出来，但是通过递归的方式，在每一层递归中都会涉及到对路径的选择和回退，从而实现了回溯的功能。

在递归函数 getPath 中，当达到叶子节点时，会将当前路径 curPath 加上当前节点的值，并将该路径添加到结果数组 res 中。然后，递归函数会立即返回。在返回之后，由于 JavaScript 中函数参数是按值传递的，而不是按引用传递，所以 curPath 不会受到影响，它的值仍然是递归调用之前的值。

具体来说，在这段代码中，curPath 的值在递归调用时会被修改，但在递归返回时不会被修改。因此，当递归返回之后，curPath 的值应该是递归调用之前的值。

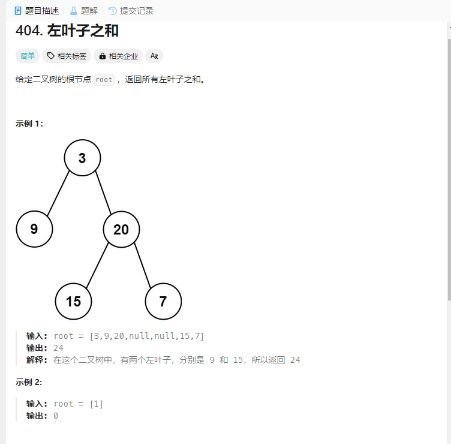
左叶子之和

题目

解法：

1.层序遍历+处理父节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var sumOfLeftLeaves = function(root) {
    let sum = 0;
    if(root == null){
        return 0;
    }
    let queue = [root];
    while(queue.length>0){
        let length = queue.length;
        for(let i = 0;i<length;i++){
        let temp = queue.shift();
        //通过节点的父节点来判断其左孩子是不是左叶子了
        if(temp.left && !temp.left.left && !temp.left.right){
            sum += temp.left.val;
        }
        if(temp.left){
            queue.push(temp.left);
        }
        if(temp.right){
            queue.push(temp.right)
        }
    }
    }
    return sum;

};

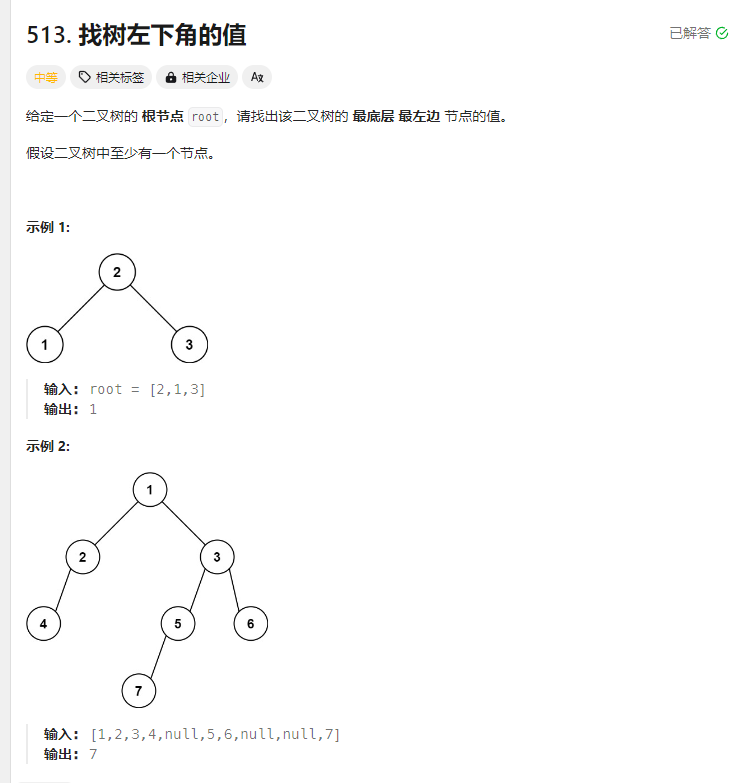
找树左下角的值

题目

解法：

1.层序遍历 + 简单判断
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var findBottomLeftValue = function(root) {
    let queue = [root];
    let result = 0;
    if(root == null){
        return 0;
    }
    while(queue.length>0){
        let length = queue.length;
        for(let i =0;i<length;i++){
            let temp = queue.shift();
            //这里result每过一层都会被覆盖，所以result的值为最后一层的最左值
            if(i == 0){
                result = temp.val;
            }
            if(temp.left){
                queue.push(temp.left);
            }
            if(temp.right){
                queue.push(temp.right);
            }
        }
    }
    return result
};




2.递归法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
//递归法
var findBottomLeftValue = function(root) {
    //首先考虑递归遍历 前序遍历 找到最大深度的叶子节点即可
    let maxPath = 0, resNode = null;
    // 1. 确定递归函数的函数参数
    const dfsTree = function(node, curPath) {
    // 2. 确定递归函数终止条件
        if(node.left === null && node.right === null) {
            if(curPath > maxPath) {
            maxPath = curPath;
            resNode = node.val;
            }
        }
        node.left && dfsTree(node.left, curPath+1);
        node.right && dfsTree(node.right, curPath+1);
    }
    dfsTree(root,1);
    return resNode;
};

扩展

怎么判断当前层数是最后一层

1
2
3
4
// 判断是否到达最后一层
       if(queue.length === 0){
           result = queue[0].val; // 更新result为最后一层的最左边节点的值
       }

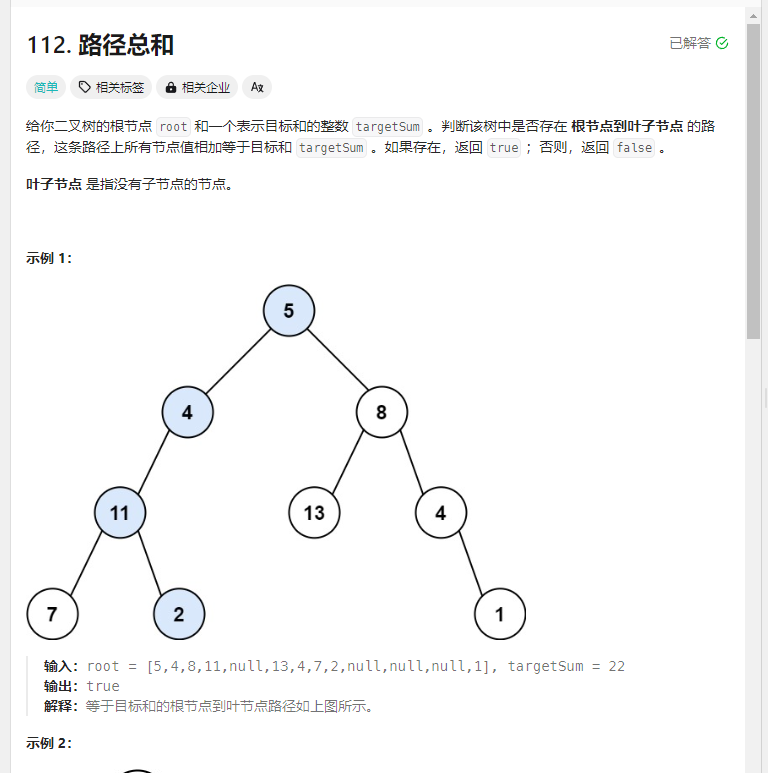
路径总和

题目

解法：

1.递归+回溯法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {boolean}
 */
var hasPathSum = function (root, targetSum) {
    let getPath = function (node, sum) {
        //防止节点为空的情况导致下面node.left和node.right访问空值
        if (node == null) {
            return false;
        }
        //递归出口
        if (node.left == null && node.right == null) {
            sum += node.val;
            if (sum == targetSum) {
                return true;
            }
        }
        //一般处理
        sum += node.val;
        //只需要一条路径满足目标之和就可，无需找到后再接着遍历其它路径
       return (getPath(node.left, sum)) || (getPath(node.right, sum));

    }
    return getPath(root, 0);

};

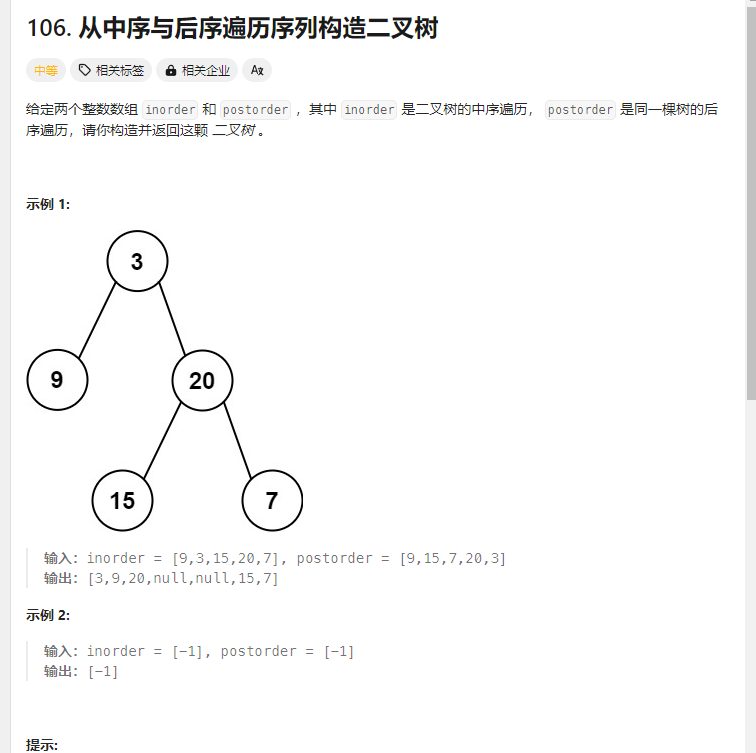
从中序与后序遍历序列构造二叉树

题目

思路：

首先回忆一下如何根据两个顺序构造一个唯一的二叉树，相信理论知识大家应该都清楚，就是以 后序数组的最后一个元素为切割点，先切中序数组，根据中序数组，反过来再切后序数组。一层一层切下去，每次后序数组最后一个元素就是节点元素。

说到一层一层切割，就应该想到了递归。

来看一下一共分几步：

  • 第一步：如果数组大小为零的话，说明是空节点了。
  • 第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。
  • 第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
  • 第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）
  • 第五步：切割后序数组，切成后序左数组和后序右数组
  • 第六步：递归处理左区间和右区间

解法：

1.节点切割左右数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} inorder
 * @param {number[]} postorder
 * @return {TreeNode}
 */
var buildTree = function(inorder, postorder) {
    //没有节点，返回了
    if(!postorder.length){
        return null;
    }
    //取出后序的最后一个节点，它为根节点
    let rootval = postorder.pop();

    //记录这个根节点在中序中的位置
    let index = inorder.indexOf(rootval);
    //新建一个中间节点
    const rootnode = new TreeNode(rootval); 
    //根据中序中的位置index 作为分割左中，右中序列的标志
    //递归操作
    rootnode.left = buildTree(inorder.slice(0,index),postorder.slice(0,index));
    rootnode.right = buildTree(inorder.slice(index+1),postorder.slice(index));

    //返回给左或右
    return rootnode;


};

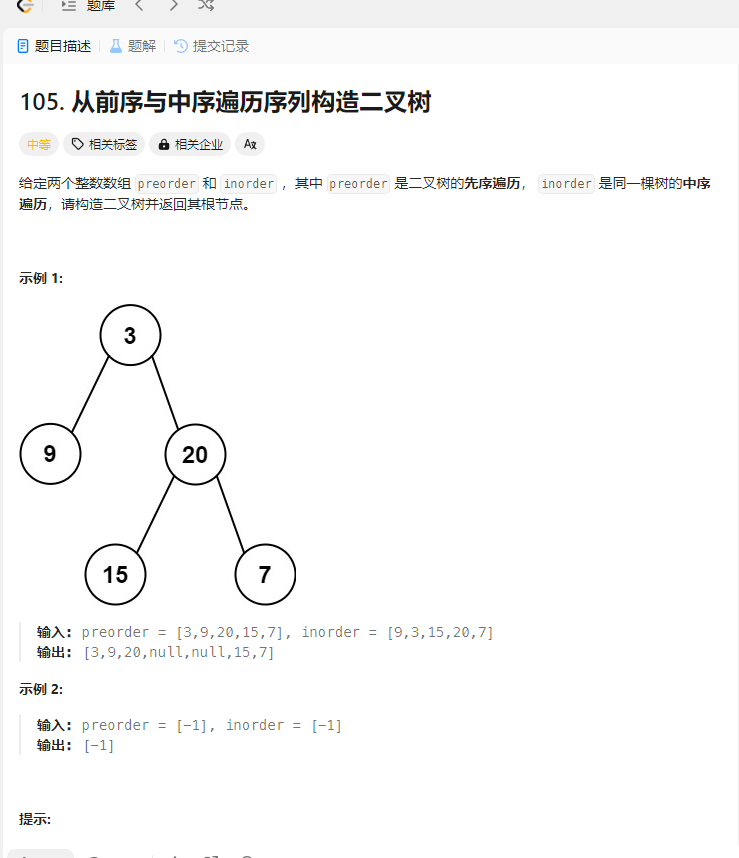
从前序与中序遍历序列构造二叉树

题目

解法：

1.节点切割左右数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} inorder
 * @param {number[]} postorder
 * @return {TreeNode}
 */
var buildTree = function(preorder, inorder)  {
    //没有节点，返回了
    if(!preorder.length){
        return null;
    }
    //取出先序的第一个节点，它为根节点
    let rootval = preorder.shift();

    //记录这个根节点在中序中的位置
    let index = inorder.indexOf(rootval);
    //新建一个中间节点
    const rootnode = new TreeNode(rootval); 
    //根据中序中的位置index 作为分割左中，右中序列的标志
    //递归操作
    //对象引用传递，所以传入的preorder一直在改变
    //这里为什么要传(0,index)而不是(1,index)，因为preorder已经弹出一个根节点元素了，所以从0开始，并不会搞到根节点
    rootnode.left = buildTree(preorder.slice(0,index),inorder.slice(0,index));
    rootnode.right = buildTree(preorder.slice(index),inorder.slice(index+1));

    //返回给左或右
    return rootnode;


};

注意点：

js不是值传递吗？为什么递归调用结束后preorder会被改变呢?

在 JavaScript 中，虽然函数参数是按值传递的，但是对于对象（包括数组）来说，传递的是引用的副本。这意味着，当你将一个对象作为参数传递给函数时，实际上传递的是该对象的引用（内存地址），而不是对象本身的副本。因此，在函数内部对该对象的修改会影响到原始对象。

在你的代码中，虽然 preorder 是一个数组，但是传递给 buildTree 函数时，实际上是传递了数组的引用。所以在递归调用中对 preorder 的修改会影响到原始的 preorder 数组。

在递归调用结束后，preorder 数组被修改的原因是因为在每次递归调用中，使用了 preorder.shift() 来取出根节点，这会改变原始的 preorder 数组，使其每次递归调用时都减少一个节点。

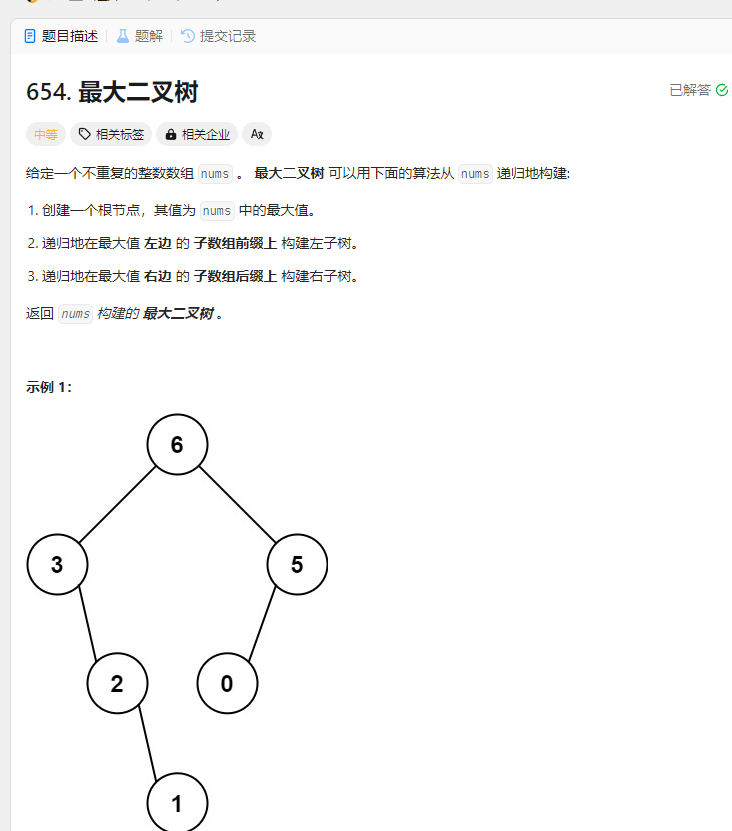
最大二叉树

题目

解法：

1.递归法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} nums
 * @return {TreeNode}
 */
var constructMaximumBinaryTree = function (nums) {
    // 递归函数，用于构建最大二叉树
    const BuildTree = (arr, left, right) => {
        // 基本情况：如果左索引大于右索引，则返回 null
        if (left > right)
            return null;

        // 初始化变量来追踪最大值及其索引
        let maxValue = -1;
        let maxIndex = -1;

        // 遍历子数组，从左索引到右索引
        for (let i = left; i <= right; ++i) {
            // 如果当前元素大于最大值，则更新最大值及其索引
            if (arr[i] > maxValue) {
                maxValue = arr[i];
                maxIndex = i;
            }
        }
        // 创建根节点，值为最大值
        let root = new TreeNode(maxValue);

        // 递归构建左子树和右子树
        root.left = BuildTree(arr, left, maxIndex - 1);
        root.right = BuildTree(arr, maxIndex + 1, right);

        return root; // 返回根节点
    }

    // 调用递归函数，构建整个数组对应的最大二叉树
    let root = BuildTree(nums, 0, nums.length - 1);

    return root; // 返回最大二叉树的根节点
};

注意点:

1
2
3
if (left > right)            
return null; 
什么时候会发生？

当递归过程中传入的左索引 left 大于右索引 right 时，意味着当前子数组为空，即没有节点需要处理。

没有需要构建的节点，因此递归可以终止，直接返回 null。这样做可以避免进一步的递归调用，从而节省时间和空间。

合并二叉树

题目

解法：

1.递归法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * @param {TreeNode} root1
 * @param {TreeNode} root2
 * @return {TreeNode}
 */
var mergeTrees = function(root1, root2){
    // mergeTrees 函数接收两个根节点 root1 和 root2 作为参数
    // 返回合并后的树的根节点
    const preOrder =  (root1, root2) => {
        // preOrder 函数用于执行先序遍历并合并两棵树
        if (!root1) {
            // 如果 root1 为空，返回 root2，表示将 root2 合并到 root1 上
            return root2;
        }
        if (!root2) {
            // 如果 root2 为空，返回 root1，表示将 root1 合并到 root2 上
            return root1;
        }
        // 如果 root1 和 root2 都不为空，则将它们的值相加
        root1.val += root2.val;
        // 递归地合并左子树和右子树
        root1.left = preOrder(root1.left, root2.left);
        root1.right = preOrder(root1.right, root2.right);
        // 返回合并后的根节点
        return root1;
    }
    // 调用 preOrder 函数，将两棵树合并成一棵树，并返回合并后的根节点
    return preOrder(root1, root2);
};

递归的终止条件:

1
2
3
4
5
6
7
8
9
10
if (!root1) {
            // 如果 root1 为空，返回 root2，表示将 root2 合并到 root1 上
            return root2;
        }
        if (!root2) {
            // 如果 root2 为空，返回 root1，表示将 root1 合并到 root2 上
            return root1;
        }
        
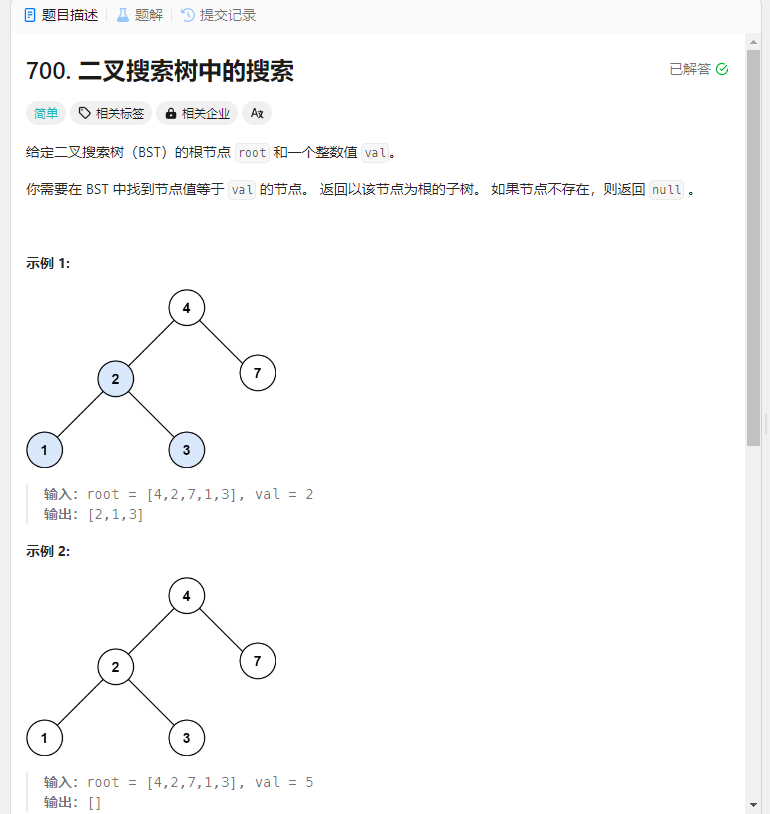
//这两个条件用于判断当其中一个树为空时，直接返回另一个树。这就是递归的终止条件之一。因为在合并两棵树的过程中，如果其中一棵树为空，则直接返回另一棵树，不再需要继续向下合并。

BST—二叉搜索树中的搜索

题目

解法：

1.递归法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * 二叉树节点的定义
 * @param {number} val - 节点的值
 * @param {TreeNode} left - 左子节点
 * @param {TreeNode} right - 右子节点
 */
function TreeNode(val, left, right) {
    this.val = (val === undefined ? 0 : val);
    this.left = (left === undefined ? null : left);
    this.right = (right === undefined ? null : right);
}

/**
 * 在二叉搜索树中搜索指定值
 * 
 * @param {TreeNode} root - 二叉搜索树的根节点
 * @param {number} val - 要搜索的值
 * @return {TreeNode} - 包含搜索值的节点，如果未找到则返回 null
 */
var searchBST = function (root, val) {
    // 如果根节点为空或者其值等于目标值，则返回根节点
    if (!root || root.val === val) {
        return root;
    }
    // 如果根节点的值大于目标值，则在左子树中搜索
    if (root.val > val)
        return searchBST(root.left, val);
    // 如果根节点的值小于目标值，则在右子树中搜索
    if (root.val < val)
        return searchBST(root.right, val);
};

2.迭代法
1
2
3
4
5
6
7
8
9
10
11
var searchBST = function (root, val) {
    while (root !== null) {
        if (root.val > val)
            root = root.left;
        else if (root.val < val)
            root = root.right;
        else 
            return root;
    }
    return null;
};

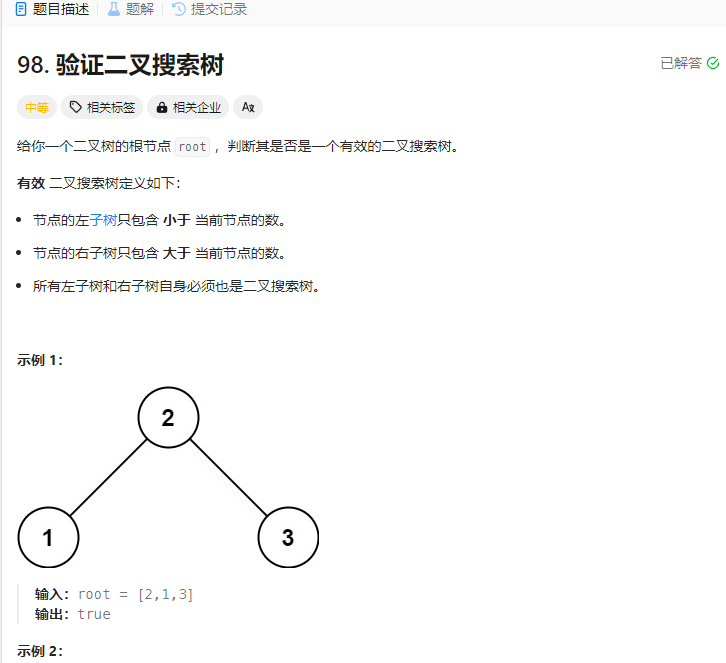
验证二叉搜索树

题目

解法：

1.中序遍历法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */

/**
 * 判断给定的二叉树是否为有效的二叉搜索树（BST）
 * 
 * @param {TreeNode} root - 二叉树的根节点
 * @return {boolean} - 如果是有效的BST，则返回true；否则返回false
 */
var isValidBST = function(root) {
    // 使用中序遍历将树变为一个有序数组
    let arr = []
    const inOrder = function(root) {
        if (root == null) {
            return;
        }
        // 中序遍历：先遍历左子树，然后访问根节点，最后遍历右子树
        inOrder(root.left);
        arr.push(root.val);
        inOrder(root.right);
    }

    // 执行中序遍历，将二叉树转换为有序数组
    inOrder(root);

    // 检查有序数组是否满足 BST 的性质
    for (let i = 0; i < arr.length - 1; i++) {
        // 如果有序数组中存在逆序，则说明不是有效的BST
        if (arr[i] >= arr[i + 1]) {
            return false;
        }
    }
    // 如果中序遍历得到的数组满足 BST 的性质，则返回true
    return true;
};

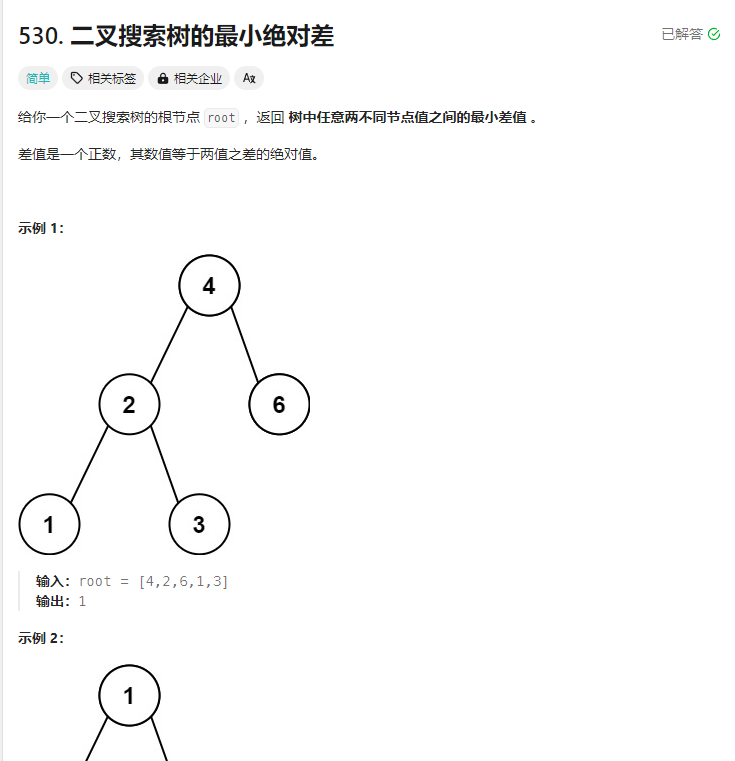
二叉搜索树的最小绝对差

题目

解法：

二叉搜索树采用中序遍历，其实就是一个有序数组。

在一个有序数组上求两个数最小差值，这是不是就是一道送分题了。

最直观的想法，就是把二叉搜索树转换成有序数组，然后遍历一遍数组，就统计出来最小差值了

1.中序遍历法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */

/**
 * 计算二叉搜索树中任意两节点的最小差值
 * 
 * @param {TreeNode} root - 二叉搜索树的根节点
 * @return {number} - 任意两节点的最小差值
 */
var getMinimumDifference = function(root) {
    // 使用中序遍历将树变为一个有序数组
    let arr = []
    const inOrder = function(root) {
        if (root == null) {
            return;
        }
        // 中序遍历：先遍历左子树，然后访问根节点，最后遍历右子树
        inOrder(root.left);
        arr.push(root.val);
        inOrder(root.right);
    }

    // 执行中序遍历，将二叉树转换为有序数组
    inOrder(root);
    
    
	//计算任意两节点的最小差值
    // 方法一:推荐
    let diff = arr[arr.length - 1]; // 初始化最小差值为数组中最后两个元素的差值
    for (let i = 1; i < arr.length; ++i) {
        // 遍历数组，计算相邻两节点的差值，并更新最小差值
        if (diff > arr[i] - arr[i - 1])
            diff = arr[i] - arr[i - 1];
    }
    return diff; // 返回最小差值
    
    //方法二:我的
     let min = arr[1] - arr[0];
     for(let i = 0;i<arr.length-1;i++){
        if(arr[i+1]-arr[i]<min){
            min = arr[i+1]-arr[i];
        }
     }
    return min;
};

二叉搜索树中的众数

题目

解法：

1.中序遍历法 + 哈希表
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/**
 * 寻找二叉搜索树中出现次数最多的节点值（众数）
 * 
 * @param {TreeNode} root - 二叉搜索树的根节点
 * @return {number[]} - 包含所有众数的数组
 */
var findMode = function (root) {
    // 用于存储中序遍历后的节点值数组
    let arr = [];

    // 中序遍历函数，将二叉搜索树转换为有序数组
    const inOrder = function (root) {
        if (root == null) {
            return;
        }
        // 先遍历左子树
        inOrder(root.left);
        // 访问当前节点
        arr.push(root.val);
        // 再遍历右子树
        inOrder(root.right);
    }

    // 执行中序遍历
    inOrder(root);
    
    // 使用 Map 存储节点值及其出现次数的映射关系
    let map = new Map();
    for (const num of arr) {
        map.set(num, (map.get(num) || 0) + 1);
    }
    
    // 找到出现次数最多的节点值的出现次数
    let maxFrequency = 0;
    for (const frequency of map.values()) {
        maxFrequency = Math.max(maxFrequency, frequency);
    }

    // 找到所有出现次数等于最大出现次数的节点值（众数）
    let modes = [];
    for (const [num, frequency] of map.entries()) {
        if (frequency === maxFrequency) {
            modes.push(num);
        }
    }

    return modes; // 返回众数数组
};

2.中序遍历+清空数组结果集
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
var findMode = function(root) {
    // 不使用额外空间，使用中序遍历,设置出现最大次数初始值为1
    let count = 0,maxCount = 1;
    let pre = root,res = [];
    // 1.确定递归函数及函数参数
    const travelTree = function(cur) {
        // 2. 确定递归终止条件
        if(cur === null) {
            return ;
        }
        travelTree(cur.left);
        // 3. 单层递归逻辑
        if(pre.val === cur.val) {
            count++;
        }else {
            count = 1;
        }
        pre = cur;
        if(count === maxCount) {
            res.push(cur.val);
        }
        if(count > maxCount) {
            res = [];
            maxCount = count;
            res.push(cur.val);
        }
        travelTree(cur.right);
    }
    travelTree(root);
    return res;
};

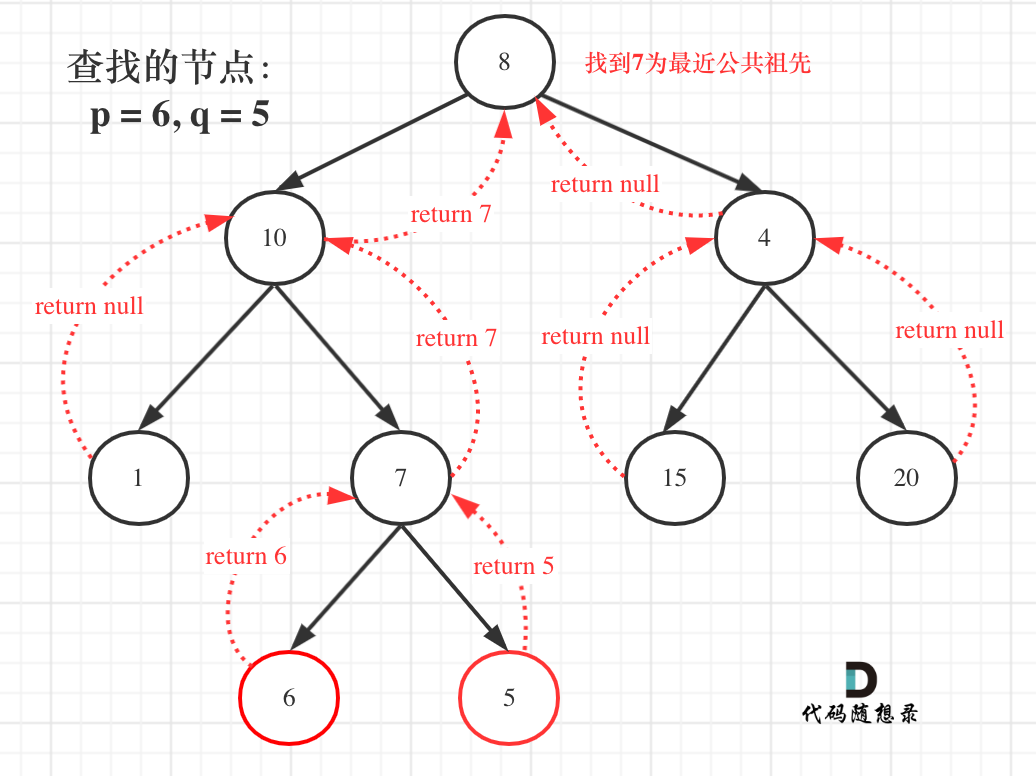
二叉树的最近公共祖先

题目

解法：

1.后序遍历整棵二叉树+递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
/**
 * 寻找二叉树中指定节点的最近公共祖先节点
 * 
 * @param {TreeNode} root - 二叉树的根节点
 * @param {TreeNode} p - 节点 p
 * @param {TreeNode} q - 节点 q
 * @return {TreeNode} - 最近公共祖先节点
 */
var lowestCommonAncestor = function(root, p, q) {
    /**
     * 后序遍历函数，寻找节点 p 和节点 q 的最近公共祖先节点
     * 
     * @param {TreeNode} root - 当前子树的根节点
     * @param {TreeNode} p - 节点 p
     * @param {TreeNode} q - 节点 q
     * @return {TreeNode} - 最近公共祖先节点
     */
    const postorderTraversal = function(root, p, q) {
        // 递归终止条件
        if (root == null || root === p || root === q) {
            return root;
        }
        // 在左子树中寻找节点 p 和节点 q 的最近公共祖先节点
        let left = postorderTraversal(root.left, p, q);
        // 在右子树中寻找节点 p 和节点 q 的最近公共祖先节点
        let right = postorderTraversal(root.right, p, q);
        // 如果左子树和右子树分别找到了节点 p 和节点 q，则当前节点即为最近公共祖先节点
        if (left !== null && right !== null) {
            return root;
        } // 如果左子树找到了节点 p 或节点 q，则返回找到的节点（可能是 p 或 q）
        else if (left !== null) {
            return left;
        } // 如果右子树找到了节点 p 或节点 q，则返回找到的节点（可能是 p 或 q）
        else if (right !== null) {
            return right;
        }else{
            return null;
        }
       
        
       
        
    }
    
    // 调用后序遍历函数寻找最近公共祖先节点
    return postorderTraversal(root, p, q);
};

二叉搜索树的最近公共祖先

题目

解法：

1.递归法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */

/**
 * 寻找二叉搜索树中两个节点的最低公共祖先节点
 * @param {TreeNode} root 二叉搜索树的根节点
 * @param {TreeNode} p 第一个节点
 * @param {TreeNode} q 第二个节点
 * @return {TreeNode} 返回最低公共祖先节点
 */
var lowestCommonAncestor = function(root, p, q) {
    // 递归终止条件：当前节点为空，返回 null
    if(root == null){
        return null;
    }
    // 如果当前节点的值大于 p 和 q 的值，说明 p 和 q 都在当前节点的左子树中
    if(root.val > p.val && root.val > q.val){
        // 递归搜索左子树
        let left = lowestCommonAncestor(root.left,p,q);
        return left; // 返回左子树的结果
    }
    // 如果当前节点的值小于 p 和 q 的值，说明 p 和 q 都在当前节点的右子树中
    if(root.val < p.val && root.val < q.val){
        // 递归搜索右子树
        let right = lowestCommonAncestor(root.right,p,q);
        return right; // 返回右子树的结果
    }

    // 如果以上情况都不满足，说明当前节点就是最低公共祖先节点
    return root;
};

2.迭代法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

var lowestCommonAncestor = function(root, p, q) {
    // 使用迭代的方法
    while(root) {
        if(root.val > p.val && root.val > q.val) {
            root = root.left;
        }else if(root.val < p.val && root.val < q.val) {
            root = root.right;
        }else {
            return root;
        }
        
    }
    return null;
};

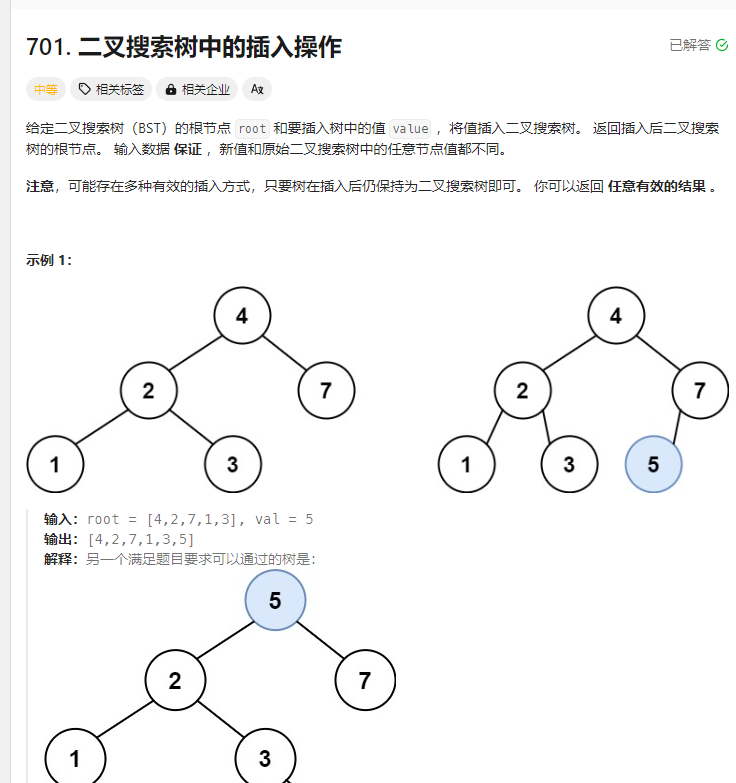
二叉搜索树中的插入操作

题目

解法：

1.迭代法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */

/**
 * 向二叉搜索树中插入一个节点
 * @param {TreeNode} root 二叉搜索树的根节点
 * @param {number} val 要插入的节点值
 * @return {TreeNode} 返回插入后的二叉搜索树的根节点
 */
// 迭代法
var insertIntoBST = function (root, val) {
    // 如果根节点为空，则直接将新节点作为根节点
    if (root == null) {
        root = new TreeNode(val);
    } else {
        let parent = new TreeNode(0); // 父节点
        let cur = root; // 当前节点
        // 循环找到要插入的位置
        while (cur) {
            parent = cur; // 更新父节点为当前节点
            if (cur.val < val) {
                cur = cur.right; // 若当前节点的值小于要插入的值，则向右子树移动
            }
            else if(cur.val > val) {
                cur = cur.left; // 若当前节点的值大于要插入的值，则向左子树移动
            }
        } 
        let node = new TreeNode(val); // 创建要插入的新节点

        // 将新节点插入到相应位置
        if (parent.val > val) {
            parent.left = node; // 若父节点的值大于要插入的值，则新节点为左子节点
        }
        if (parent.val < val) {
            parent.right = node; // 若父节点的值小于要插入的值，则新节点为右子节点
        }
    } 
    return root; // 返回根节点
};

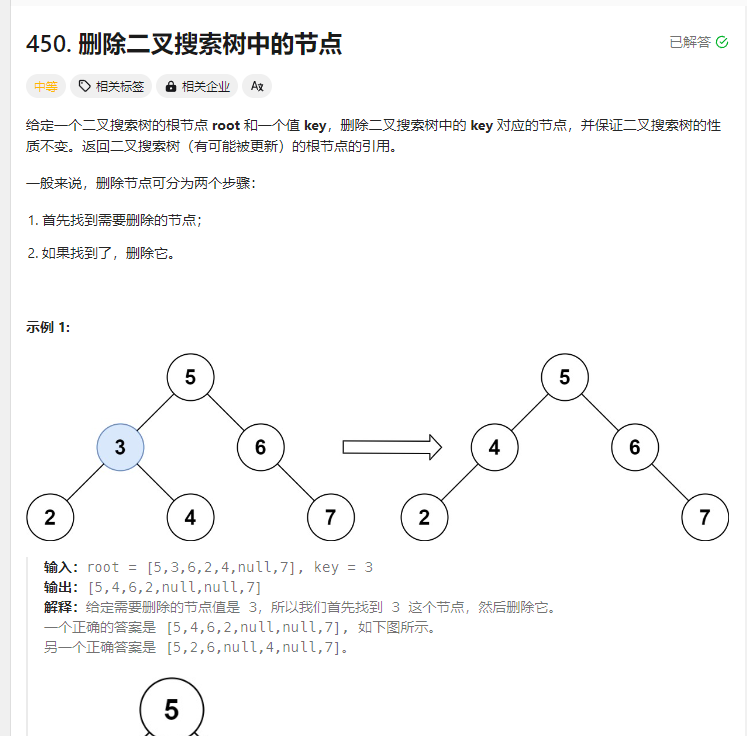
删除二叉搜索树中的节点

题目

解法：

要分类讨论，删除节点会改变树的结构

1.递归法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

var deleteNode = function(root, key) {
    const deleteTraseval = function(node, key) {
        if (node === null) {
            return null;
        }
        
        // 当前节点值比要删除的值大，继续向左子树搜索
        if (node.val > key) {
            node.left = deleteTraseval(node.left, key);
            return node;
        }
        // 当前节点值比要删除的值小，继续向右子树搜索
        else if (node.val < key) {
            node.right = deleteTraseval(node.right, key);
            return node;
        }
        // 找到要删除的节点
        else {
            // 情况一：叶子节点
            if (!node.left && !node.right) {
                return null;
            }
            // 情况二：左子树有，右子树没有
            else if (node.left && !node.right) {
                return node.left;
            }
            // 情况三：右子树有，左子树没有
            else if (!node.left && node.right) {
                return node.right;
            }
            // 情况四：左右子树都有
            else {
                let cur = node.right;
                while (cur.left) {
                    cur = cur.left;
                }
                // 将左子树连接到当前节点的右子树中
                cur.left = node.left;
                // 返回右子树作为删除节点后的树的根节点
                return node.right;
            }
        }
    };

   return deleteTraseval(root, key);
    
};

回溯

回溯三部曲：

  • 回溯函数模板返回值以及参数

  • 回溯函数终止条件

  • 回溯搜索的遍历过程

回溯法模板

1
2
3
4
5
6
7
8
9
10
11
12
void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

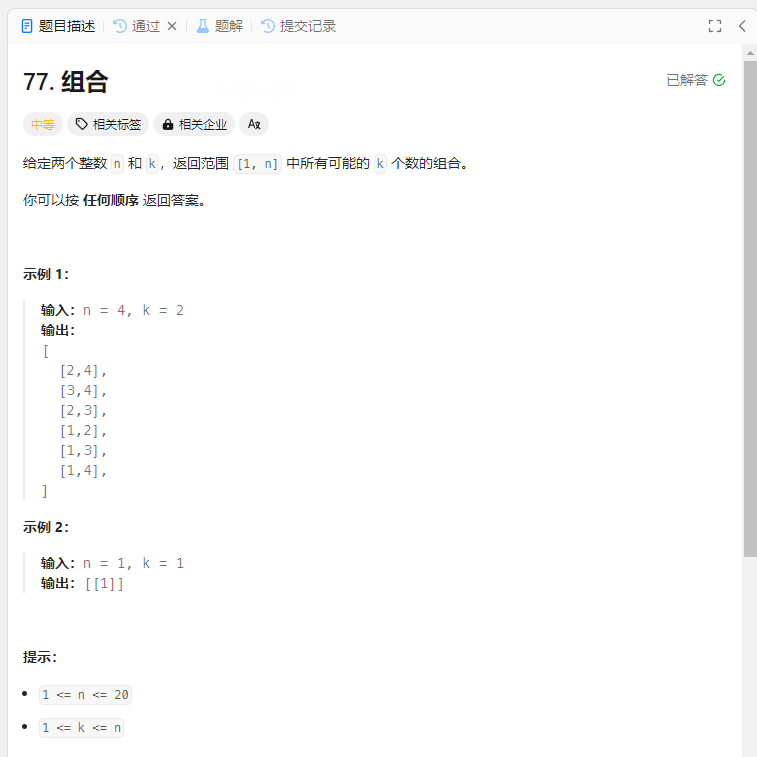
组合

题目

解法：

回溯法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
let result = []  // 用于存储所有的组合结果
let path = []    // 用于存储当前组合

// 主函数，n表示数字的范围是从1到n，k表示组合的长度
var combine = function(n, k) {
  result = []  // 清空结果数组，确保每次调用函数时都是空的
  combineHelper(n, k, 1)  // 调用辅助函数开始递归，初始startIndex为1
  return result  // 返回所有的组合结果
};

// 辅助递归函数
const combineHelper = (n, k, startIndex) => {
  if (path.length === k) {  // 如果当前组合的长度等于k
    result.push([...path])  // 将当前组合拷贝到结果数组中
    return  // 结束当前递归
  }
  // 循环从startIndex到n - (k - path.length) + 1
  // n - (k - path.length) + 1 的目的是减少不必要的计算
  for (let i = startIndex; i <= n - (k - path.length) + 1; ++i) {
    path.push(i)  // 将当前数字添加到当前组合中
    combineHelper(n, k, i + 1)  // 递归调用，下一个数字从i + 1开始
    path.pop()  // 从当前组合中移除最后一个数字，回溯
  }
}

组合总和Ⅲ

题目

解法：

回溯法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * @param {number} k
 * @param {number} n
 * @return {number[][]}
 */
let path = [];  // 用于存储当前组合
let result = [];  // 用于存储所有符合条件的组合

// 主函数，k表示组合的长度，n表示组合的和
var combinationSum3 = function(k, n) {
    result = [];  // 清空结果数组，确保每次调用函数时都是空的
    combineSum(k, n, 1);  // 调用辅助函数开始递归，初始startIndex为1
    return result;  // 返回所有符合条件的组合
};

// 辅助函数，用于计算数组中所有元素的和
const sum  = (nums) => {
    return nums.reduce((p, c) => p + c, 0);
}

// 辅助递归函数
const combineSum = (k, n, startIndex) => {
    // 如果当前组合的长度等于k且组合的和等于n
    if (path.length === k && sum(path) === n) {
        result.push([...path]);  // 将当前组合拷贝到结果数组中
        return;  // 结束当前递归
    }
    
    // 如果当前组合的长度已经等于k但和不等于n，或者和已经超过n
    if (path.length >= k || sum(path) >= n) {
        return;  // 提前结束递归，避免不必要的计算
    }

    // 循环从startIndex到9 - (k - path.length) + 1
    // 9 - (k - path.length) + 1 的目的是减少不必要的计算
    for (let i = startIndex; i <= 9; ++i) {
        path.push(i);  // 将当前数字添加到当前组合中
        combineSum(k, n, i + 1);  // 递归调用，下一个数字从i + 1开始
        path.pop();  // 从当前组合中移除最后一个数字，回溯
    }
}

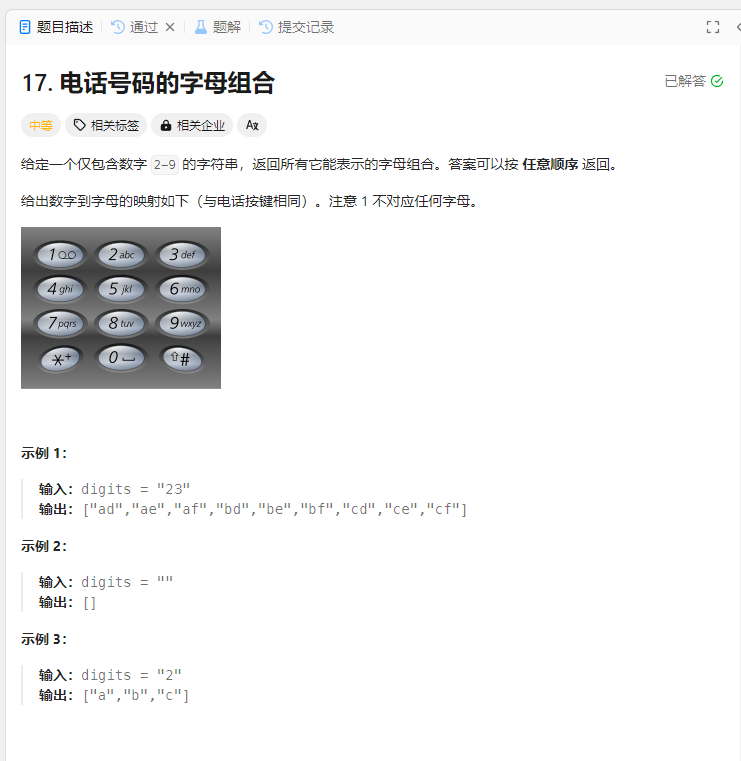
电话号码的字母组合

题目

解法：

回溯法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/**
 * @param {string} digits - 输入的数字字符串
 * @return {string[]} - 返回所有可能的字母组合
 */
var letterCombinations = function (digits) {
    // 数字到字母的映射表，索引对应数字键盘上的数字
    const map = ['', '', 'abc', 'def', 'ghi', 'jkl', 'mno', 'pqrs', 'tuv', 'wxyz'];
    
    let result = [], path = [];
    const len = digits.length;

    // 如果输入为空字符串，直接返回空数组
    if (!len) {
        return [];
    }

    // 如果输入只有一个数字，直接返回该数字对应的字母数组
    if (len == 1) {
        return map[digits].split("");
    }

    // 递归生成组合
    backCombine(digits, len, 0);
    return result;

    /**
     * 递归函数，用于生成字母组合
     * @param {string} digits - 输入的数字字符串
     * @param {number} k - 输入的长度
     * @param {number} a - 当前处理的索引
     */
    function backCombine(digits, k, a) {
        // 如果当前索引等于输入长度，说明已经生成一个完整的组合
        if (a === k) {
            result.push(path.join("")); // 将组合加入结果数组
            return;
        } else {
            // 遍历当前数字对应的所有字母
            for (const v of map[digits[a]]) {
                path.push(v); // 将当前字母加入路径
                backCombine(digits, len, a + 1); // 递归处理下一个数字
                path.pop(); // 回溯，移除当前字母
            }
        }
    }
};

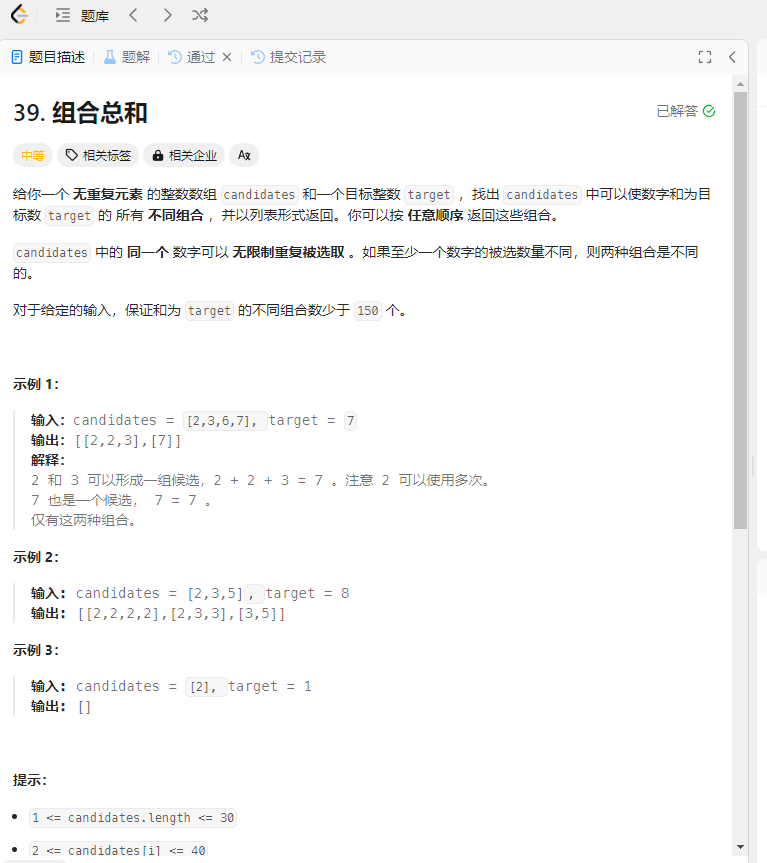
组合总和

题目

解法：

回溯法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
 * @param {number[]} candidates
 * @param {number} target
 * @return {number[][]}
 */
let result = [], path = [];
var combinationSum = function (candidates, target) {
    result = [];
    candidates.sort((a, b) => a - b); //这个是为了后面剪枝

    const combine2 = function (sum, startIndex) {
        if (sum > target) {
            return;
        }
        if (sum === target) {
            result.push([...path]);
        }
        for (let i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++) {
            const k = candidates[i];
            if (sum + k > target) {
                break;
            }
            sum += k;
            path.push(k);
            combine2(sum, i);
            path.pop();
            sum -= k;
        }
    }
    combine2(0, 0);
    return result;
};

组合总和Ⅱ

题目

解法

回溯法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * @param {number[]} candidates 候选数数组
 * @param {number} target 目标和
 * @return {number[][]} 组合结果数组
 */
let result = [], path = [];
let used = [];
var combinationSum2 = function(candidates, target) {
    result = [];  // 初始化结果数组
    candidates.sort((a, b) => a - b);  // 将候选数组排序

    const combine3 = function(sum, startIndex) {
        if (sum > target) {
            return;  // 如果当前和大于目标值，则返回
        }
        if (sum === target) {
            result.push([...path]);  // 如果当前和等于目标值，则将当前路径添加到结果数组
            return;
        }

        // 遍历候选数组，从startIndex开始
        for (let j = startIndex; j < candidates.length && sum + candidates[j] <= target; j++) { 
            const k = candidates[j];  
            // 如果当前元素与前一个元素相同，跳过以避免重复组合
            if (j > startIndex && candidates[j] === candidates[j - 1]) {
                continue;
            }
            if (sum + k > target) {
                break;  // 如果当前和加上k大于目标值，退出循环
            }
            sum += k;  // 更新当前和
            path.push(k);  // 将当前元素添加到路径中
            combine3(sum, j + 1);  // 递归调用，查找下一层组合
            path.pop();  // 回溯，移除路径中的最后一个元素
            sum -= k;  // 恢复当前和
        }
    }

    combine3(0, 0);  // 从0和索引0开始
    return result;  // 返回结果数组
};

分割回文串

题目

解法

回溯法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
/**
 * @param {string} s 输入字符串
 * @return {string[][]} 分割后的回文子字符串数组
 */
let result = [], path = [];

// 判断子字符串s[l...r]是否为回文
const isPalindrome = function(s, l, r) {
    while (l < r) {
        if (s[l] !== s[r]) { // 如果左右字符不相等，则不是回文
            return false;
        }
        l++; // 左指针右移
        r--; // 右指针左移
    }
    return true; // 所有字符匹配，则是回文
};

var partition = function(s) {
    result = []; // 初始化结果数组
    
    const divide = function(s, startindex) {
        // 如果起始索引超过或等于字符串长度，说明已处理完所有字符
        if (startindex >= s.length) {
            result.push([...path]); // 将当前路径（一个分割方案）加入结果数组
            return;
        }
        
        // 从起始索引开始遍历字符串的每个子字符串
        for (let i = startindex; i < s.length; i++) {
            // 如果当前子字符串是回文
            if (isPalindrome(s, startindex, i)) {
                path.push(s.slice(startindex, i + 1)); // 将当前子字符串加入路径
                divide(s, i + 1); // 递归处理剩余字符串
                path.pop(); // 回溯，移除路径中的最后一个子字符串
            }
        }
    };

    divide(s, 0); // 从字符串的第一个字符开始分割
    return result; // 返回所有的分割方案
};

动态规划

动规五部曲：

  1. 确定dp数组（dp table）以及下标的含义
  2. 确定递推公式
  3. dp数组如何初始化
  4. 确定遍历顺序
  5. 举例推导dp数组

斐波那契数

题目

解法：

1.动态规划法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
var fib = function(n) {
    if(n==0){
        return 0;
    }
    let dp = new Array(n + 1);
    dp[0] = 0;
    dp[1] = 1;
    for(let i=2;i<=n;i++){
       let sum = dp[0] + dp[1];
       dp[0] = dp[1];
       dp[1] = sum;
    }

    return dp[1];
    
};

这是一道非常简单的入门题目

dp[i]的定义为：第i个数的斐波那契数值是dp[i]

状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];

dp数组如何初始化 

1
2
dp[0] = 0;
dp[1] = 1;

从dp[i] = dp[i - 1] + dp[i - 2];中可以看出，dp[i]是依赖 dp[i - 1] 和 dp[i - 2]，那么遍历的顺序一定是从前到后遍历的

爬楼梯

题目

解法：

1.动态规划法
1
2
3
4
5
6
7
8
9
10
11
12
//动态规划解
var climbStairs = function(n) {
    let dp = new Array(n + 1);
        dp[1] = 1;
        dp[2] = 2;
        
        for (let i = 3; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        
        return dp[n];
    };

常规解法可以分成多个子问题，爬第n阶楼梯的方法数量，等于 2 部分之和

1
2
3
4
爬上 n−1阶楼梯的方法数量。因为再爬1阶就能到第n阶
爬上 n−2阶楼梯的方法数量，因为再爬2阶就能到第n阶
所以我们得到公式 dp[n]=dp[n−1]+dp[n−2]
同时需要初始化 dp[0]=1 和 dp[1]=1

使用最小花费爬楼梯

题目

解法：

如果代码写出来了，一直AC不了，灵魂三问：

  1. 这道题目我举例推导状态转移公式了么？
  2. 我打印dp数组的日志了么？
  3. 打印出来了dp数组和我想的一样么？
1.动态规划法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

var minCostClimbingStairs = function(cost) {
    //定义数组
    let dp = new Array(cost.length+1);
    //初始化
    dp[0] = 0;
    dp[1] = 0;
    //遍历
    for(let i = 2;i<=cost.length;i++){
        //状态转移方程
        dp[i] = Math.min((dp[i-1]+cost[i-1]),(dp[i-2]+cost[i-2]));

    }
    //返回结果
    return dp[cost.length];

};

不同路径

题目

解法：

1.动态规划法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * @param {number} m
 * @param {number} n
 * @return {number}
 */
var uniquePaths = function(m, n) {
    //定义二维数组
    const dp = Array(m).fill().map(item => Array(n));
    //初始化列
    for(let j = 0;j<n;j++){
        dp[0][j] = 1;
    }
    //初始化行
    for(let i = 0;i<m;i++){
        dp[i][0] = 1
    }
    //遍历
    for(let i = 1;i<m;i++){
        for(let j = 1;j<n;j++){
            //状态转移方程
            dp[i][j] = dp[i-1][j] + dp[i][j-1];
        }
    }
    //返回值
    return dp[m-1][n-1]

};

不同路径 II

题目

解法：

1.动态规划法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * @param {number[][]} obstacleGrid
 * @return {number}
 */
var uniquePathsWithObstacles = function(obstacleGrid) {

    // 初始化
    //从给定数组找长度
    const m = obstacleGrid.length;
    const n = obstacleGrid[0].length;
    //要填充0，注意！！！题目要求
    const dp = Array(m).fill().map(() => Array(n).fill(0));

    // 初始化第一列
    for(let i = 0; i < m && obstacleGrid[i][0] === 0; i++){
        dp[i][0] = 1;
    }

    // 初始化第一行
    for(let j = 0; j < n && obstacleGrid[0][j] === 0; j++){
        dp[0][j] = 1;
    }

    // 遍历
    for(let i = 1; i < m; i++){
        for(let j = 1; j < n; j++){
            if(obstacleGrid[i][j] === 1){
                // 遇到障碍置 0
                dp[i][j] = 0;
            } else {
                // 状态转移方程
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
    }

    // 返回值
    return dp[m - 1][n - 1];
};



整数拆分

题目

解法：

1.动态规划法
1
2
3
4
5
6
7
8
9
10
11
12
var integerBreak = function(n) {
   let dp = new Array(n+1).fill(0);
   dp[0] = 0;
   dp[1] = 0;
   dp[2] = 1
   for(let i = 3;i<=n;i++){
    for(let j = 1;j<=i/2;j++){ //整数拆分的重点在于拆分成若干个 近似相同的数，所以超出i/2的不会是最大
        dp[i] = Math.max(j * (i-j),j * dp[i-j],dp[i]);//这里分别是拆分两个数，拆分三个数及以上，不拆分的情况分类
    }
   }
   return dp[n]
};

0/1背包问题

题目

解法

1.二维数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
function testWeightBagProblem (weight, value, size) {
    //定义dp数组
    const len = weight.length;
    console.log(len);
    let dp = new Array(len).fill().map(()=> Array(size+1).fill(0));

    //初始化dp
    for(let i = 0; i < len; i++){
        dp[i][0] = 0;
    }
    for(let j = 0; j < weight[0]; j++){
        dp[0][j] = 0;
    }
    for(let j = weight[0];j<=size;j++){
        dp[0][j] = value[0];
    }

    //递推方程
    for(let i = 1;i<len;i++){
        for(let j = 0;j<=size;j++){
            if(j<weight[i]){
                dp[i][j] = dp[i-1][j];
            }else{
                dp[i][j] = Math.max(dp[i-1][j],dp[i][j-weight[i]]+value[i]);
            }
        }
    }

    console.table(dp);
}

function test () {
    console.log(testWeightBagProblem([1, 3, 4, 5], [15, 20, 30, 55], 6));
}

test();
2.一维滚动数组
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
function testWeightBagProblem(wight, value, size) {
  const len = wight.length, 
    dp = Array(size + 1).fill(0);
  for(let i = 1; i <= len; i++) {	//必须先物品再背包容量
    for(let j = size; j >= wight[i - 1]; j--) { //这里要倒序遍历，防止物品被重复装入
      dp[j] = Math.max(dp[j], value[i - 1] + dp[j - wight[i - 1]]);
    }
  }
  return dp[size];
}


function test () {
  console.log(testWeightBagProblem([1, 3, 4, 5], [15, 20, 30, 55], 6));
}

test();

分割等和子集

题目

解法

动态规划法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * @param {number[]} nums
 * @return {boolean}
 */
var canPartition = function (nums) {
    let len = nums.length;
    let sum = nums.reduce((prev, cur) => prev + cur, 0);
    
    // 如果总和是奇数，直接返回 false
    if (sum % 2 !== 0) {
        return false;
    }
    
    let target = sum / 2;
    let dp = new Array(target + 1).fill(0);
    
    // 初始化
    dp[0] = 0;
    
    // 遍历
    for (let i = 0; i < len; i++) {
        for (let j = target; j >= nums[i]; j--) {
            // 状态转移方程
            dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
            if (dp[j] === target) {
                return true;
            }
        }
    }

    return dp[target] === target;
};